题目内容
13.设无穷等比数列{an}的公比为q,若a1=$\lim_{n→∞}({a_3}+{a_4}+…+{a_n})$,则q=$\frac{{\sqrt{5}-1}}{2}$.分析 由于q为无穷等比数列{an}的公比,即有0<|q|<1,由无穷等比数列的极限公式可得$\underset{lim}{n→∞}$(a3+a4+…+an)=$\frac{{a}_{3}}{1-q}$,再由等比数列的通项公式,解方程可得公比q.
解答 解:由于q为无穷等比数列{an}的公比,即有0<|q|<1,
由${a_1}=\lim_{n→∞}({a_3}+{a_4}+…+{a_n})$,可得
a1=$\frac{{a}_{3}}{1-q}$=$\frac{{a}_{1}{q}^{2}}{1-q}$,
即为q2+q-1=0,
解得q=$\frac{\sqrt{5}-1}{2}$($\frac{-1-\sqrt{5}}{2}$舍去),
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查数列的极限的求法,注意运用无穷等比数列的极限公式,考查运算能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
5.观察下面的几何体,哪些是棱柱( )


| A. | ①③⑤ | B. | ①⑥ | C. | ①③⑥ | D. | ③④⑥ |
20.函数$y=\frac{{\sqrt{4-{x^2}}}}{{1-{x^2}}}$的定义域为( )
| A. | [-2,2] | B. | [-2,-1)∪(-1,1)∪(1,2] | C. | (-∞,-2)∪(2,+∞) | D. | [-2,-1)∪(1,2] |
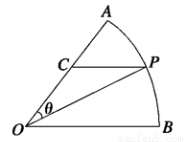
 ,圆心角
,圆心角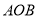 的大小等于
的大小等于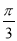 ,半径为
,半径为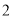 百米,在半径
百米,在半径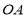 上取一点
上取一点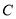 ,过点
,过点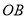 的直线交弧
的直线交弧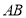 于点
于点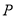 .设
.设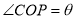 .
.
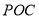 面积
面积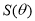 的函数表达式.
的函数表达式.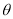 的值.
的值.