题目内容
16.已知数列{an}中,a1=2,且$2{a_n}={a_{n-1}}+1({n≥2,n∈{N^+}})$.(I)求证:数列{an-1}是等比数列,并求出数列{an}的通项公式;
(Ⅱ)设bn=n(an-1),数列{bn}的前n项和为Sn,求证:1≤Sn<4.
分析 (I)利用递推关系变形可得an-1=$\frac{1}{2}({a}_{n-1}-1)$,即可证明;
(II)利用“错位相减法”、等比数列的前n项和公式、数列的单调性即可证明.
解答 证明:(I)${a_n}-1=(\frac{1}{2}{a_{n-1}}+\frac{1}{2})-1=\frac{1}{2}({a_{n-1}}-1)$,又a1-1=1≠0
∴数列{an-1}是首项为1,公比为2的等比数列.
∴${a_n}-1={({\frac{1}{2}})^{n-1}}$,得${a_n}={({\frac{1}{2}})^{n-1}}+1$.
(II)${b_n}=n({a_n}-1)=n{({\frac{1}{2}})^{n-1}}$,
设${S_n}=1+\frac{2}{2}+\frac{3}{2^2}+\frac{4}{2^3}+…+\frac{n-1}{{{2^{n-2}}}}+\frac{n}{{{2^{n-1}}}}$…①
则$\frac{1}{2}{S_n}=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+\frac{4}{2^4}+…+\frac{n-1}{{{2^{n-1}}}}+\frac{n}{2^n}$…②
①-②得:$\frac{1}{2}{S_n}=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+…+\frac{1}{{{2^{n-1}}}}-\frac{n}{2^n}=2-\frac{1}{{{2^{n-1}}}}-\frac{n}{2^n}$,
∴${S_n}=4-\frac{2}{{{2^{n-1}}}}-\frac{n}{{{2^{n-1}}}}=4-\frac{2+n}{{{2^{n-1}}}}$,
${S_n}=4-\frac{2+n}{{{2^{n-1}}}}<4$,又${b_n}=n{({\frac{1}{2}})^{n-1}}>0$,
∴数列{Sn}是递增数列,故Sn≥S1=1,
∴1≤Sn<4.
点评 本题考查了“错位相减法”、等比数列的前n项和公式、数列的单调性、递推关系,考查了推理能力与计算能力,属于中档题.

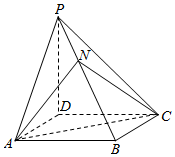 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )| A. | 1:2 | B. | 1:8 | C. | 1:6 | D. | 1:3 |
| A. | (-$\frac{1}{4}$,+∞) | B. | (-∞,-$\frac{1}{4}$) | C. | (0,+∞) | D. | (-∞,0) |
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
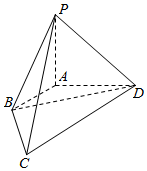 如图,在四棱锥P-ABCD中,已知棱AB,AD,AP两两垂直,长度分别为1,2,2.若$\overrightarrow{DC}$=λ$\overrightarrow{AB}$,且向量$\overrightarrow{PC}$与$\overrightarrow{BD}$夹角的余弦值为$\frac{\sqrt{15}}{15}$.
如图,在四棱锥P-ABCD中,已知棱AB,AD,AP两两垂直,长度分别为1,2,2.若$\overrightarrow{DC}$=λ$\overrightarrow{AB}$,且向量$\overrightarrow{PC}$与$\overrightarrow{BD}$夹角的余弦值为$\frac{\sqrt{15}}{15}$. 在图中的算法中,如果输入A=2016,B=98,则输出的结果是14.
在图中的算法中,如果输入A=2016,B=98,则输出的结果是14.