题目内容
7.C331+C332+C333+…+C3333除以9的余数是( )| A. | 7 | B. | 0 | C. | -1 | D. | -2 |
分析 C331+C332+C333+…+C3333=(1+1)33-1=(9-1)11-1,利用二项式定理展开即可得出.
解答 解:C331+C332+C333+…+C3333=(1+1)33-1=233-1=(9-1)11-1=${9}^{11}-{∁}_{11}^{1}{9}^{10}$+…+${∁}_{11}^{10}×9$-2=9$({9}^{10}-{∁}_{11}^{1}{9}^{9}+…+{∁}_{11}^{10})$-9+7.
∴C331+C332+C333+…+C3333除以9的余数是7.
故选:A.
点评 本题考查了二项式定理的应用、整除的知识,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
4.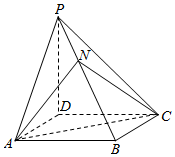 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )
 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )| A. | 1:2 | B. | 1:8 | C. | 1:6 | D. | 1:3 |