题目内容
已知数列{an}满足:a1=1,且an,an+1,
成等差数列.又正项数列{bn}满足b1=e,且
是bn与bn+1的等比中项.
(1)求证:{2n-1an}为等差数列,并求出数列{an}的通项公式;
(2)求证?n∈N*都有
-1≤lnb1+lnb2+…+lnbn.
| 1 |
| 2n-1 |
| bn+1 |
(1)求证:{2n-1an}为等差数列,并求出数列{an}的通项公式;
(2)求证?n∈N*都有
| n+1 |
| an+1 |
考点:数列与不等式的综合,等差数列的性质
专题:等差数列与等比数列
分析:(1)由an,an+1,
成等差数列,可得2an+1=an+
,等式两边同时乘以2n-1,得2nan+1=2n-1an+1,可得{2n-1an}是等差数列,利用通项公式即可得出.
(2)即证2n-1≤lnb1+lnb2+…+lnbn.
是bn与bn+1的等比中项的等比中项,等价于b n+1=bn2+bn
当n=1时,所证的不等式易证成立
当n≥2时,b n+1=bn2+bn >bn2,∴lnbn+1>2lnbn,经放缩后证明.
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
(2)即证2n-1≤lnb1+lnb2+…+lnbn.
| bn+1 |
当n=1时,所证的不等式易证成立
当n≥2时,b n+1=bn2+bn >bn2,∴lnbn+1>2lnbn,经放缩后证明.
解答:
证明:(1)∵an,an+1,
成等差数列,
∴2an+1=an+
等式两边同时乘以2n-1,得2nan+1=2n-1an+1
∴{2n-1an}是等差数列,公差为1
又a1=1,∴20a0=1
∴2n-1an=1+(n-1)×1=n,
∴an=
;
(2)∵
=2n,
∴?n∈N*都有
-1≤lnb1+lnb2+…+lnbn.?2n-1≤lnb1+lnb2+…+lnbn.
∵
是bn与bn+1的等比中项的等比中项,等价于b n+1=bn2+bn .
∵4e>8,∴b1>
=1,b1+1=
<e.
∴lnb1>ln1=0=21-1-1,lnb1<ln(b1+1)<1=21-1,故当n=1时,所证的不等式成立.
当n≥2时,b n+1=bn2+bn >bn2,∴lnbn+1>2lnbn.
∴lnbn>2lnbn-1>…>2n-2lnb2=2n-2.
∴lnb1+lnb2+…+lnbn>0+1+2+…+2n-1=2n-1
| 1 |
| 2n-1 |
∴2an+1=an+
| 1 |
| 2n-1 |
等式两边同时乘以2n-1,得2nan+1=2n-1an+1
∴{2n-1an}是等差数列,公差为1
又a1=1,∴20a0=1
∴2n-1an=1+(n-1)×1=n,
∴an=
| n |
| 2n-1 |
(2)∵
| n+1 |
| an+1 |
∴?n∈N*都有
| n+1 |
| an+1 |
∵
| bn+1 |
∵4e>8,∴b1>
-1+
| ||
| 2 |
| e |
| b1 |
∴lnb1>ln1=0=21-1-1,lnb1<ln(b1+1)<1=21-1,故当n=1时,所证的不等式成立.
当n≥2时,b n+1=bn2+bn >bn2,∴lnbn+1>2lnbn.
∴lnbn>2lnbn-1>…>2n-2lnb2=2n-2.
∴lnb1+lnb2+…+lnbn>0+1+2+…+2n-1=2n-1
点评:本题是数列与不等式的综合题.考查数列性质的判定,通项公式求解,放缩法证明不等式,数列求和.此类题联通了高中数学主干知识和方法,是高考中常见的命题立意形式.

练习册系列答案
相关题目
 一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )
一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )| A、9+π | B、6+π |
| C、6+3π | D、9+3π |
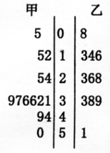 如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图,则甲运动员的得分的中位数是
如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图,则甲运动员的得分的中位数是 在三棱锥A-BCD中,AB⊥AC,AB⊥AD,AC⊥AD,AB=AC=1,AD=2,E、F分别是BC、BD的中点.
在三棱锥A-BCD中,AB⊥AC,AB⊥AD,AC⊥AD,AB=AC=1,AD=2,E、F分别是BC、BD的中点. M、N是正方体ABCD-A1B1C1D1的棱A1B1、A1D1的中点,如图是用过M、N、A和D、N、C1的平面截去两个角后所得几何体,该几何体的主视图是( )
M、N是正方体ABCD-A1B1C1D1的棱A1B1、A1D1的中点,如图是用过M、N、A和D、N、C1的平面截去两个角后所得几何体,该几何体的主视图是( )


