题目内容
17.已知a<0,则“ax0=b”的充要条件是( )| A. | ?x∈R,$\frac{1}{2}$ax2-bx≥$\frac{1}{2}$ax02-bx0 | B. | ?x∈R,$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax02-bx0 | ||
| C. | ?x∈R,$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax02-bx0 | D. | ?x∈R,$\frac{1}{2}$ax2-bx≥$\frac{1}{2}$ax02-bx0 |
分析 a<0,令f(x)=$\frac{1}{2}$ax2-bx,利用导数可得:x=$\frac{b}{a}$函数f(x)的极大值点即最大值点,即可判断出结论.
解答 解:a<0,令f(x)=$\frac{1}{2}$ax2-bx,则f′(x)=ax-b,令f′(x)=0,解得x=$\frac{b}{a}$.
∴x=$\frac{b}{a}$函数f(x)的极大值点即最大值点,
∴?x∈R,$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax02-bx0,
∴a<0,则“ax0=b”的充要条件是:?x∈R,$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax02-bx0,
故选:C.
点评 本题考查了利用导数研究函数的单调性极值与最值、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.过双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3{a}^{2}}$=1(a>0)的右顶点A作斜率为-1的直线,该直线与Γ的渐近线交于B、C两点(点B在第一象限,点C在第二象限),则$\frac{|BC|}{|AB|}$=( )
| A. | 1+$\sqrt{2}$ | B. | 1+$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$+$\sqrt{3}$ |
12.已知ω>0,函数$f(x)=sin({ωx-\frac{π}{3}})$在$({\frac{π}{3},\frac{π}{2}})$上单调递减,则ω的取值范围是( )
| A. | $[{\frac{5}{2},\frac{11}{3}}]$ | B. | $[{\frac{1}{2},\frac{3}{4}}]$ | C. | $({0,\frac{1}{2}}]$ | D. | $({0,\frac{11}{3}}]$ |
2.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)单调递减,若实数a满足f(log3a)+f(${log_{\frac{1}{3}}}a$)≥2f(1),则a的取值范围是( )
| A. | (0,3] | B. | (0,$\frac{1}{3}$] | C. | [$\frac{1}{3}$,3] | D. | [1,3] |
9.已知平面向量$\overrightarrow a$=(0,-1),$\overrightarrow b$=(1,1),|λ$\overrightarrow a$+$\overrightarrow b$|=$\sqrt{5}$,则λ的值为( )
| A. | 3 | B. | 2 | C. | 3或-1 | D. | 2或-1 |
7.已知不等式|x-2|<3的解集为A,函数y=ln(1-x)的定义域为B,则图中阴影部分表示的集合为( )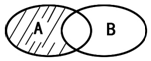

| A. | {x∈R|-1<x<1} | B. | {x∈R|1≤x<5} | C. | {x∈R|1<x<5} | D. | {x∈R|x≥1} |