题目内容
已知等比数列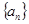 的首项
的首项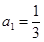 ,公比
,公比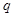 满足
满足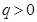 且
且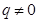 ,又已知
,又已知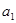 ,
, ,
,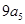 ,成等差数列;
,成等差数列;
求数列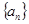 的通项;
的通项;
令 ,求
,求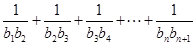 的值;
的值;
(1) ;(2)
;(2) ;
;
解析试题分析:(1)利用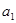 ,
, ,
,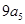 成等差数列得到一个式子,然后将式子中的
成等差数列得到一个式子,然后将式子中的 ,
, 换成
换成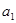 ,
,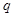 得出
得出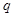 ,通项公式得解;(2)把(1)问中求得的
,通项公式得解;(2)把(1)问中求得的 代入式子
代入式子 得
得 的通项公式,将通项代入
的通项公式,将通项代入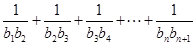 得到
得到 ,通过观察可发现求这个式子的和可以通过列项求和得到;
,通过观察可发现求这个式子的和可以通过列项求和得到;
试题解析:(1)解:在等比数列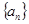 中,
中, ,
, 成等差数列,
成等差数列,
即: 
 解得:
解得:
又



(2)解:


=
= =
=
考点:1、等差数列及等比数列的通项及性质;2、对数的运算;3、列项求和;

练习册系列答案
相关题目
 的前
的前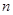 项和为
项和为 ,且
,且 ,数列
,数列 中,
中,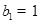 ,点
,点 在直线
在直线 上.
上. 的通项
的通项 和
和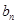 ;
; ,求数列
,求数列 的前n项和
的前n项和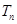 .
.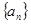 满足:
满足: ,
,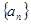 的前
的前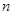 项和为
项和为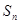 .
.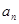 及
及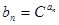 (其中
(其中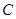 为常数,且
为常数,且 ),求证数列
),求证数列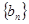 为等比数列.
为等比数列.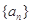 中,
中,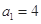 .(1)若
.(1)若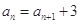 ,求
,求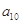 ;(2)若数列
;(2)若数列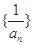 为等差数列,且
为等差数列,且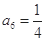 ,求数列
,求数列 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数 的图象上
的图象上 归纳数列
归纳数列 ),
), ,
, ,
, ;
; ,
, ,
, ,
, ;
; ,…..,
,….., ,
, 的值;
的值;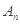 为数列
为数列 的前
的前 对一切
对一切 ,求
,求 的取值范围
的取值范围 中,
中, ,
,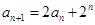 .
. .证明:数列
.证明:数列 是等差数列;(2)求数列
是等差数列;(2)求数列 项和
项和 .
.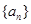 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
, ,
,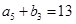 ,
,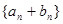 的前
的前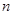 项和
项和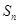 .
. 中,若
中,若 ,则
,则 的值为 .
的值为 .