题目内容
已知数列 的前
的前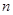 项和为
项和为 ,且
,且 =
= ,数列
,数列 中,
中,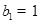 ,点
,点 在直线
在直线 上.
上.
(1)求数列 的通项
的通项 和
和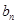 ;
;
(2) 设 ,求数列
,求数列 的前n项和
的前n项和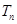 .
.
(1)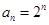 ,
,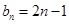 ;(2)
;(2)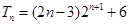
解析试题分析:(1)先由第n项与前n项关系,求出数列{ }的递推关系
}的递推关系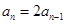 ,再由等比数列的定义判定数列{
,再由等比数列的定义判定数列{ }是等比数列,用等比数列的通项公式,求出数列{
}是等比数列,用等比数列的通项公式,求出数列{ }的通项公式,由点
}的通项公式,由点 在直线
在直线 上得,
上得,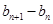 =2,根据等差数列定义知数列{
=2,根据等差数列定义知数列{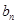 }是等差数列,所以再根据等比数列的通项公式,求出
}是等差数列,所以再根据等比数列的通项公式,求出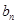 的通项公式;(2)由(1)知
的通项公式;(2)由(1)知 是等差数列与等比数列对应项乘积构成的新数列,其求和用错位相减法.
是等差数列与等比数列对应项乘积构成的新数列,其求和用错位相减法.
试题解析:(1)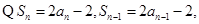
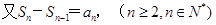 2分
2分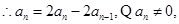 .
. 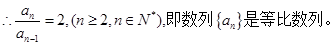 3分
3分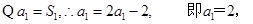
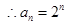
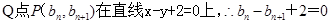
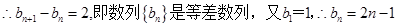 7分
7分
(2)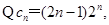
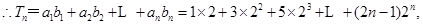
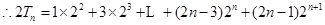 9分
9分
因此: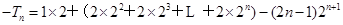 10分
10分
即: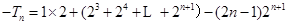
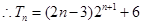
考点:数列第n项与前n项和的关系;等差数列定义与通项公式;等比数列定义与通项公式;错位相减法;转化思想;运算求解能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 }中,
}中, =14,前10项和
=14,前10项和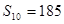 .
.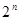 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前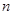 项和
项和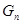 .
. 满足:
满足: ,
,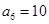 .
.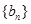 的各项均为正数,
的各项均为正数,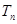 为其前
为其前 项和,若
项和,若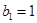 ,
,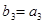 ,求
,求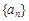 的前n项和为
的前n项和为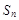 ,且
,且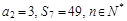
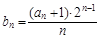 ,求数列
,求数列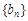 的前n项和Tn.
的前n项和Tn.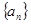 中,
中,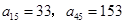 ,求数列
,求数列
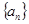 的首项
的首项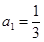 ,公比
,公比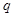 满足
满足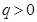 且
且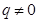 ,又已知
,又已知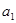 ,
, ,
,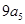 ,成等差数列;
,成等差数列; ,求
,求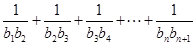 的值;
的值;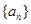 的首项为23,公差为整数,且第6项为正数,从第7项起为负数。
的首项为23,公差为整数,且第6项为正数,从第7项起为负数。 是正数时,求n的最大值。
是正数时,求n的最大值。 +n-4.
+n-4.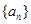 为等差数列,
为等差数列,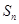 为其前
为其前 项和,若
项和,若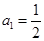 ,
,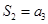 ,则
,则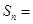 ___________.
___________.