题目内容
13.现有四个推理:①在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;
②由“若数列{an}为等差数列,则有$\frac{{a}_{6}+{a}_{7}+…+{a}_{10}}{5}$=$\frac{{a}_{1}+{a}_{2}+…+{a}_{15}}{15}$成立”类比“若数列{bn}为等比数列,则有$\root{5}{{b}_{6}{b}_{7}…{b}_{10}}$=$\root{15}{{b}_{1}{b}_{2}…{b}_{15}}$成立”;
③由实数运算中,(a•b)•c=a•(b•c),可以类比得到在向量中,($\overrightarrow{a}•\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}•\overrightarrow{c}$),
④在实数范围内“5-3=2>0⇒5>3”,类比在复数范围内,“5+2i-(3+2i)=2>0⇒5+2i>3+2i”;
则得出的结论正确的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由三角形对应四面体,边类比面,即可判断①;由等差数列和等比数列的类比特点:和与积对应,除数对应根指数,即可判断②;由向量数量积为实数,以及向量共线定理,即可判断③;由复数范围内,两数均为实数,才好比较,虚数不能比较,即可判断④.
解答 解:①在平面内“三角形的两边之和大于第三边”,由边类比面,类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”,故正确;
②由“若数列{an}为等差数列,则有$\frac{{a}_{6}+{a}_{7}+…+{a}_{10}}{5}$=$\frac{{a}_{1}+{a}_{2}+…+{a}_{15}}{15}$成立”,由类比规则:和与积对应,除数对应根指数,类比“若数列{bn}为等比数列,则有$\root{5}{{b}_{6}{b}_{7}…{b}_{10}}$=$\root{15}{{b}_{1}{b}_{2}…{b}_{15}}$成立”,
故正确;
③由实数运算中,(a•b)•c=a•(b•c),在向量中,($\overrightarrow{a}•\overrightarrow{b}$)•$\overrightarrow{c}$与$\overrightarrow{c}$共线,$\overrightarrow{a}$•($\overrightarrow{b}•\overrightarrow{c}$)与$\overrightarrow{a}$共线,故不正确;
④在实数范围内“5-3=2>0⇒5>3”,由在复数范围内,虚数不能比较大小,类比在复数范围内,“5+2i-(3+2i)=2>0⇒5+2i>3+2i”,故不正确.
其中正确的个数为2.
故选:C.
点评 本题考查命题的真假判断和应用,主要是类比推理的应用,注意类比规则,以及等差数列和等比数列的特点和两数的大小比较,考查推理和判断能力,属于中档题.

 中国古代数学名著《九章算术》中记载了公元前344年商鞅造的一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取为3,其体积为12.6(立方升),则三视图中x的为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅造的一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取为3,其体积为12.6(立方升),则三视图中x的为( )| A. | 3.4 | B. | 4.0 | C. | 3.8 | D. | 3.6 |
| A. | 8π | B. | 12π | C. | 8$\sqrt{3}$π | D. | 12$\sqrt{3}$π |
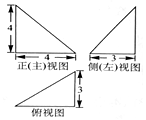 某四面体三视图如图所示,该四面体的体积为( )
某四面体三视图如图所示,该四面体的体积为( )| A. | 8 | B. | 10 | C. | 20 | D. | 24 |
| A. | $\frac{{x}^{2}}{21}-\frac{{y}^{2}}{28}$=1 | B. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{28}-\frac{{y}^{2}}{21}$=1 | D. | $\frac{{x}^{2}}{3}-\frac{{y}^{2}}{4}$=1 |
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |