题目内容
11.将函数f(x)=sin(x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{6}$个单位后的图象关于y轴对称,则函数f(x)在[0,$\frac{π}{2}$]上的最小值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 根据平移后的函数为偶函数求出φ的值,得出f(x)的解析式,利用正弦函数的单调性得出f(x)的最小值.
解答 解:将函数f(x)向右平移$\frac{π}{6}$个单位后得函数g(x)=f(x-$\frac{π}{6}$)=sin(x+φ-$\frac{π}{6}$),
∵g(x)关于y轴对称,∴φ$-\frac{π}{6}$=$\frac{π}{2}+kπ$,即φ=$\frac{2π}{3}$+kπ.
∵|φ|<$\frac{π}{2}$,∴φ=$-\frac{π}{3}$.
∴f(x)=sin(x-$\frac{π}{3}$).
∵x∈[0,$\frac{π}{2}$],∴x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{π}{6}$].
∴当x-$\frac{π}{3}$=-$\frac{π}{3}$时,f(x)取得最小值-$\frac{\sqrt{3}}{2}$.
故选:D.
点评 本题考查了函数的图象变换,正弦函数的图象与性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.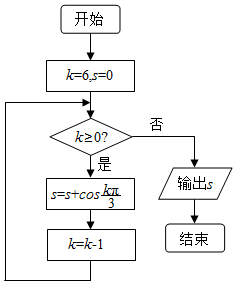 执行如图所示的程序框图,则输出s的值等于( )
执行如图所示的程序框图,则输出s的值等于( )
 执行如图所示的程序框图,则输出s的值等于( )
执行如图所示的程序框图,则输出s的值等于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |