题目内容
12.已知点F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是钝角三角形,则该双曲线的离心率e的取值范围是( )| A. | (1,+∞) | B. | (1,2) | C. | (1,1+$\sqrt{2}$) | D. | (2,+∞) |
分析 利用双曲线的对称性可得∠AEB是钝角,得到|AF|>|EF|,求出|AF|,|CF|,得到关于a,b,c的不等式,求出离心率的范围.
解答 解:∵双曲线关于x轴对称,且直线AB垂直x轴,
∴∠AEF=∠BEF,
∵△ABE是钝角三角形,
∴∠AEB是钝角,即有|AF|>|EF|,
∵F为左焦点,过F且垂直于x轴的直线与双曲线交于A、B两点,
∴|AF|=$\frac{{b}^{2}}{a}$,
∵|EF|=a+c,
∴$\frac{{b}^{2}}{a}$>a+c,即c2-ac-2a2>0,
由e=$\frac{c}{a}$,可得e2-e-2>0,
解得e>2或e<-1(舍去),
则双曲线的离心率的范围是(2,+∞).
故选:D.
点评 本题考查双曲线的对称性、双曲线的三参数关系:c2=a2+b2,双曲线的离心率问题就是研究三参数a,b,c的关系.

练习册系列答案
相关题目
17.双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1的实轴长为( )
| A. | 6 | B. | 3 | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
1.与椭圆$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1有相同的焦点,且经过点P($\sqrt{2}$,-$\sqrt{2}$)的双曲线的离心率为( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
2.集合A={a1,a2}的子集的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
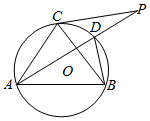 如图,圆O是△ABC的外接圆,点D是劣弧$\widehat{BC}$的中点,连结AD并延长,与以C为切点的切线交于点P,求证:$\frac{PC}{PA}=\frac{BD}{AC}$.
如图,圆O是△ABC的外接圆,点D是劣弧$\widehat{BC}$的中点,连结AD并延长,与以C为切点的切线交于点P,求证:$\frac{PC}{PA}=\frac{BD}{AC}$.