题目内容
在△ABC中,设![]() ·
·![]() =
=![]() ·
·![]() .
.
(1)求证:△ABC为等腰三角形;
(2)若|![]() +
+![]() |=2且B∈[
|=2且B∈[![]() ,
,![]() ],求
],求![]() ·
·![]() 的取值范围
的取值范围
(1)因为![]() ·
·![]() =
=![]() ·
·![]() ,所以
,所以![]() ·(
·(![]() -
-![]() )=0,又
)=0,又![]() +
+![]() +
+![]() =0,
=0,
所以![]() =-(
=-(![]() +
+![]() ),所以-(
),所以-(![]() +
+![]() )·(
)·(![]() -
-![]() )=0.所以
)=0.所以![]() 2-
2-![]() 2=0,
2=0,
所以|![]() |2=|
|2=|![]() |2,即|
|2,即|![]() |=|
|=|![]() |,故△ABC为等腰三角形.
|,故△ABC为等腰三角形.
(2)因为B∈[![]() ,
,![]() ],所以cosB∈[-
],所以cosB∈[-![]() ,
,![]() ],
],
设|![]() |=|
|=|![]() |=a,因为|
|=a,因为|![]() +
+![]() |=2,
|=2,
所以|![]() +
+![]() |2=4,所以a2+a2+2a2cosB=4,所以a2=
|2=4,所以a2+a2+2a2cosB=4,所以a2=![]() ,所以
,所以![]() ·
·![]() =|
=|![]() |·|
|·|![]() |cosB=
|cosB=![]() =2-
=2-![]() ∈[-2,
∈[-2,![]() ].
].
【方法技巧】解答向量与三角函数相结合问题的一般步骤
(1)利用向量的各种运算法则,常见的有a∥b,a⊥b等,去掉向量这层“外衣”,得到一个表达式.
(2)根据表达式的特![]() 点,进行有效地转化、变形、化简.
点,进行有效地转化、变形、化简.
(![]() 3)若研究三角函数的性质,需变成“三个一”的结构形式(即一个角、一次幂、一个名的形式);若研究三角形的边角关系,则需借助正、余弦定理进行求解.
3)若研究三角函数的性质,需变成“三个一”的结构形式(即一个角、一次幂、一个名的形式);若研究三角形的边角关系,则需借助正、余弦定理进行求解.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 如图,在△ABC中,设
如图,在△ABC中,设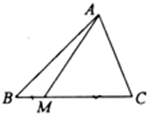 (2012•莆田模拟)如图,在△ABC中,点M在BC边上且满足CM=3MB,设
(2012•莆田模拟)如图,在△ABC中,点M在BC边上且满足CM=3MB,设