题目内容
3.用四种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色,则涂色方法总数是120.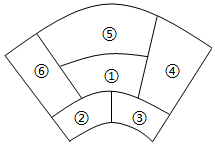
分析 根据题意,结合题意中图形的位置关系,由分类计数原理计算可得答案
解答 解:第一类:若区域6与区域4相同,涂区域5有4种方法,涂区域1有3种方法,涂区域4有2种方法,涂区域3有2种方法,涂区域2有1种方法
则不同的涂色方案的种数为4×3×2×2×1=48种;
第二类:若区域6与区域4不相同,涂区域5有4种方法,涂区域1有3种方法,涂区域4有2种方法,涂区域6有1种方法,
再分类,若涂区域3和6一样,涂区域2有2种方法,涂区域3和6不一样,涂区域3,2有1种方法,
则不同的涂色方案的种数为4×3×2×1×(2+1)=72种;
根据分类计数原理,共有72+48=120种,
故答案为:120.
点评 本题考查分类和分步计数原理的运用,注意结合题意分析所给的图形区域中的相邻位置关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.设随机变量ξ服从正态分布N(3,4),若p(ξ<2a-1)=p(ξ>a+2),则a=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
12.方程组$\left\{\begin{array}{l}{x-y-1=0}\\{2x+y-2=0}\end{array}\right.$的解集是①{1,0};②{x=1或y=0};③{(1,0)};④{(x,y)|x=1且y=0}.其中表示正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
13.已知集合A={0,a,a2},且1∈A,则a=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |