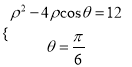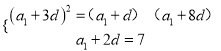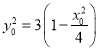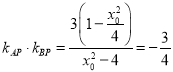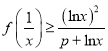题目内容
【题目】在△ABC中,tanA=![]() ,tanB=
,tanB=![]() .
.
(1)求C的大小;
(2)若△ABC的最小边长为![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用诱导公式、两角和的正切公式,求得tanC=-tan(A+B)的值,可得C的值.
(2)根据三个角的正切值,可以得到a最小,利用同角三角函数的基本关系求出 sinA、sinB的值,再利用正弦定理求出c的值,进而可得△ABC的面积.
解:(1)△ABC中,∵tanA=![]() ,tanB=
,tanB=![]() ,
,
∴tanC=-tan(A+B)=-![]() =-1,
=-1,
![]()
∴C=![]() .
.
(2)∵tanA<tanB,
∴A<B<C,
∴a为最小边,a=![]() .
.
由tanA=![]() =
=![]() ,tanB=
,tanB=![]() =
=![]() ,
,
sin2A+cos2A=1,sin2B+cos2B=1,
![]()
![]() sinA=
sinA=![]() ,sinB=
,sinB=![]() ,
,
由正弦定理,![]() =
=![]() ,可得c=
,可得c=![]() =
=![]() =
=![]() ,
,
∴△ABC的面积为![]() acsinB=
acsinB=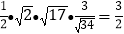 .
.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目