题目内容
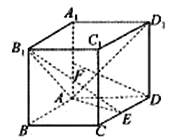
【题目】过原点的一条直线与椭圆![]() =1(a>b>0)交于A,B两点,以线段AB为直径的圆过该椭圆的右焦点F2,若∠ABF2∈[
=1(a>b>0)交于A,B两点,以线段AB为直径的圆过该椭圆的右焦点F2,若∠ABF2∈[![]() ],则该椭圆离心率的取值范围为( )
],则该椭圆离心率的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
以AB为直径的圆的圆周角∠ABF2∈[![]() ],故圆心角
],故圆心角![]() ,所以当斜率存在时,斜率
,所以当斜率存在时,斜率![]() ,然后将斜率
,然后将斜率![]() 转化为
转化为![]() 的关系式,求解离心率的取值范围;当斜率不存在时,易得
的关系式,求解离心率的取值范围;当斜率不存在时,易得![]() ,易解离心率的值,综上便可得出答案。
,易解离心率的值,综上便可得出答案。
解:当过原点的直线斜率不存在时,
因为以AB为直径的圆经过右焦点,
所以有![]() ,此时
,此时![]() ;
;
当过原点的直线斜率存在时,设过原点的直线为![]() ,
,![]() ,
,
因为∠ABF2∈[![]() ]
]
所以圆心角![]() ,
,
所以![]() ,即
,即![]() ,
,
直线与椭圆联立方程组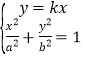 ,解得
,解得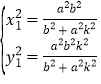 ,
,
因为以AB为直径的圆经过右焦点,
所以,以AB为直径的圆方程为![]() ,
,
所以有![]() ,
,
即![]() ,
,
故![]() ,即
,即![]() ,
,
所以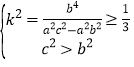 ,解得
,解得 ![]()
故得到![]()
综上:![]() ,故选B
,故选B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目