题目内容
已知函数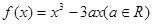
（1）当
时，求
在
的最小值；
（2）若直线
对任意的
都不是曲线
的切线，求
的取值范围；
（3）设
，求
的最大值
的解析式
（1）-2
（2）
（3）
解析试题分析：解：（1）
时，
令
2分
又
，
在的最小值为-2 4分
（2）直线的斜率为-1，由题意，方程
无实数解 6分
即
无实数解，即
无实数解，
，解得 8分
（3）由题意
，只需要求
上的最大值
且
当
10分
当
令
又由
，
的图像如图所示
当
12分
当
，的最大值在
中取得
以下解不等式
当
时，原不等式可化为
解得：
当
时，原不等式可化为
，此式无解
当时，
当
时，
14分
综上： 16分
考点：导数的运用
点评：主要是考查了导数几何意义以及导数判定函数单调性以及最值的运用，属于中档题。
练习册系列答案
名校课堂系列答案
相关题目
，
取得极值，求实数
的值；
时，求
上的最小值；
，直线
都不是曲线
的切线，求实数
在点
处取得极小值－4，使其导数
的
的取值范围为
，求：
的解析式；
，求
的最大值；
在点
处取得极小值－4，使其导数
的
的取值范围为
，求：
的解析式；
，求
的最大值；
．
在点
处的切线方程；
为曲线
的切线，且经过原点，求直线
的方程及切点坐标
的导数
为实数，
.
且与曲线
的方程；
，试判断函数
的极值点个数。
.
奇偶性, 并求出函数
的单调区间； 
有零点，求实数
的取值范围.
，
的单调递减区间；
上的最大值为20，求它在该区间的最小值 
，
，（
）．
的极值；
，函数
， 
，判断并证明
的单调性；
，试比较
与
，并加以证明．