题目内容
已知函数 在点
在点 处取得极小值-4,使其导数
处取得极小值-4,使其导数 的
的 的取值范围为
的取值范围为 ,求:
,求:
(1) 的解析式;
的解析式;
(2) ,求
,求 的最大值;
的最大值;
(1)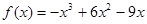
(2)m<2,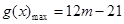 ;当m>3时,
;当m>3时,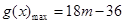 ;当
;当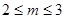 时,
时,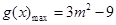
解析试题分析:⑴根据题意,由于函数 在点
在点 处取得极小值-4,
处取得极小值-4,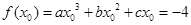
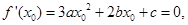 使其导数
使其导数 的
的 的取值范围为
的取值范围为 ,可知
,可知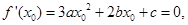 的两个根为1,3,结合韦达定理可知
的两个根为1,3,结合韦达定理可知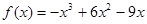
⑵由于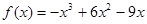 ,那么导数
,那么导数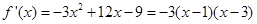
 ,求
,求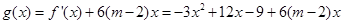 ,结合二次函数开口方向向下,以及对称轴和定义域的关系分情况讨论可知:
,结合二次函数开口方向向下,以及对称轴和定义域的关系分情况讨论可知:
①当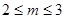 时,
时,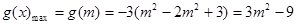
②当m<2时,g(x)在[2,3]上单调递减,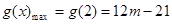
③当m>3时,g(x)在[2,3]上单调递增,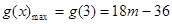
考点:导数的运用
点评:主要是考查了导数的几何意义,以及运用导数来求解函数最值的运用,属于中档题。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
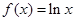 ,
,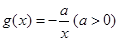
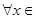 (0,e],都有f(x)≥g(x)+
(0,e],都有f(x)≥g(x)+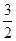 ,求实数a的取值范围.
,求实数a的取值范围. .
. 的斜率为负数时,求
的斜率为负数时,求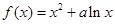 的图象在点
的图象在点 处的切线斜率为
处的切线斜率为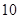 .
.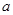 的值;
的值;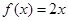 根的个数,证明你的结论;
根的个数,证明你的结论; ,使得曲线
,使得曲线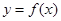 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.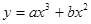 ,当
,当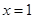 时,有极大值
时,有极大值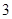 ;
;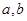 的值;
的值;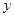 的极小值。
的极小值。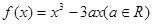
 时,求
时,求 在
在 的最小值;
的最小值; 对任意的
对任意的 都不是曲线
都不是曲线 的切线,求
的切线,求 的取值范围;
的取值范围; ,求
,求 的最大值
的最大值 的解析式
的解析式

 ,试确定函数
,试确定函数 的单调区间;
的单调区间; ,且对于任意
,且对于任意 ,
, 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围; ,求证:
,求证: .
. .
. 的单调区间;
的单调区间; 时,判断
时,判断 和
和 的大小,并说明理由;
的大小,并说明理由; 时,关于
时,关于 的方程:
的方程: 在区间
在区间 上总有两个不同的解.
上总有两个不同的解.