题目内容
(本小题满分12分)
如图,在多面体 中,平面
中,平面 ∥平面
∥平面 ,
, ⊥平面
⊥平面 ,
, ,
, ,
,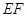 ∥
∥ .
.
且 ,
,  .
.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: ∥平面
∥平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
如图,在多面体
 中,平面
中,平面 ∥平面
∥平面 ,
, ⊥平面
⊥平面 ,
, ,
, ,
,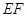 ∥
∥ .
.且
 ,
,  .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求证:
 ∥平面
∥平面 ;
;(Ⅲ)求二面角
 的余弦值.
的余弦值.(Ⅰ) 平面
平面 ∥平面
∥平面 ,
, ∥
∥ ,又
,又 四边形
四边形 为平行四边形,
为平行四边形, ∥
∥ ,
, 面
面 平面
平面
(Ⅱ)设 的中点为
的中点为 ,连接
,连接 ,则
,则 ,
, ∥
∥ ,∴四边形
,∴四边形 是平行四边形,∴
是平行四边形,∴ ∥
∥ ,由(Ⅰ)知,
,由(Ⅰ)知, 为平行四边形,∴
为平行四边形,∴ ∥
∥ ,∴
,∴ ∥
∥ ,∴
,∴ ∥
∥ ,又
,又 平面
平面 ,故
,故  ∥平面
∥平面 ;
;
(Ⅲ)- .
.
 平面
平面 ∥平面
∥平面 ,
, ∥
∥ ,又
,又 四边形
四边形 为平行四边形,
为平行四边形, ∥
∥ ,
, 面
面 平面
平面
(Ⅱ)设
 的中点为
的中点为 ,连接
,连接 ,则
,则 ,
, ∥
∥ ,∴四边形
,∴四边形 是平行四边形,∴
是平行四边形,∴ ∥
∥ ,由(Ⅰ)知,
,由(Ⅰ)知, 为平行四边形,∴
为平行四边形,∴ ∥
∥ ,∴
,∴ ∥
∥ ,∴
,∴ ∥
∥ ,又
,又 平面
平面 ,故
,故  ∥平面
∥平面 ;
;(Ⅲ)-
 .
.试题分析:(Ⅰ)
 平面
平面 ∥平面
∥平面 ,平面
,平面 平面
平面 ,平面
,平面 平面
平面 ,
, ∥
∥ ………1分
………1分又
 四边形
四边形 为平行四边形,
为平行四边形, ∥
∥ ……2分
……2分 面
面 平面
平面 ……3分
……3分
(Ⅱ)设
 的中点为
的中点为 ,连接
,连接 ,则
,则 ,
, ∥
∥ ,∴四边形
,∴四边形 是平行四边形…………4分
是平行四边形…………4分∴
 ∥
∥ ,由(Ⅰ)知,
,由(Ⅰ)知, 为平行四边形,∴
为平行四边形,∴ ∥
∥ ,∴
,∴ ∥
∥ ,
,∴四边形
 是平行四边形,…………5分
是平行四边形,…………5分即
 ∥
∥ ,又
,又 平面
平面 ,故
,故  ∥平面
∥平面 ;…………6分
;…………6分
(Ⅲ)由已知,
 两两垂直,建立如图的空间坐标系,则
两两垂直,建立如图的空间坐标系,则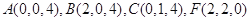 ∴
∴
设平面
 的法向量为
的法向量为 ,则
,则 ,
,令
 ,则
,则 ,而平面
,而平面 的法向量
的法向量
∴
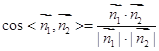 =
=
由图形可知,二面角
 的余弦值-
的余弦值- .……………………12分
.……………………12分点评:高考中常考查空间中平行关系与垂直关系的证明以及几何体体积的计算,这是高考的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理.

练习册系列答案
相关题目
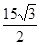 ,
,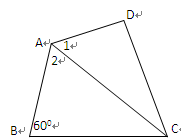
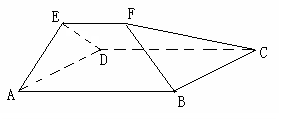
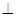 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,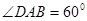 .
.
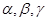 是三个不重合的平面,l是直线,给出下列命题:
是三个不重合的平面,l是直线,给出下列命题: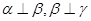 ,则
,则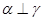 ; ②若
; ②若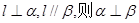
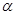 的距离相等,则
的距离相等,则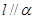 ; ④若
; ④若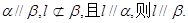
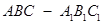 中,△
中,△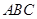 是边长为
是边长为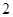 的等边三角形,
的等边三角形,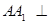 平面
平面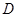 ,
,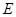 分别是
分别是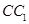 ,
,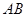 的中点.
的中点. 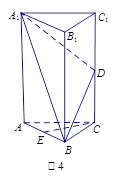
 ∥平面
∥平面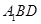 ;
;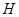 为
为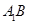 上的动点,当
上的动点,当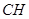 与平面
与平面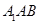 所成最大角的正切值为
所成最大角的正切值为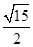 时,
时, 的底面
的底面 为平行四边形,
为平行四边形, 分别是棱
分别是棱 的中点,平面
的中点,平面 与平面
与平面 交于
交于 ,求证:
,求证:
 平面
平面 中,
中, ,
, ,
, 分别是面
分别是面 ,面
,面 的中心,则
的中心,则 和
和 所成的角为( )
所成的角为( )




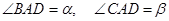 ,
,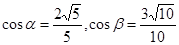 .
.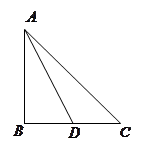
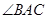 的大小;
的大小;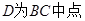 时,判断
时,判断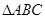 的形状,并求
的形状,并求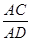 的值.
的值.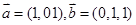 那么这条斜线与平面所成的角是 ____________
那么这条斜线与平面所成的角是 ____________