题目内容
如果平面的一条斜线和它在这个平面上的射影的方向向量分别是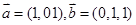 那么这条斜线与平面所成的角是 ____________
那么这条斜线与平面所成的角是 ____________
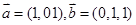 那么这条斜线与平面所成的角是 ____________
那么这条斜线与平面所成的角是 ____________ 
试题分析:根据题意可知,由于已知平面的一条斜线和它在这个平面上的射影的方向向量分别是
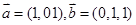 ,那么结合向量的数量积公式可知,
,那么结合向量的数量积公式可知, ,可知向量的夹角为
,可知向量的夹角为 ,即为这条斜线与平面所成的角是
,即为这条斜线与平面所成的角是 。故答案为
。故答案为 。
。点评:对于斜线与平面所成的角冠军艾女士对于平面的射影的确定,然后结合法向量与平面的斜向量坐标关系,结合数量积公式得到夹角。属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,平面
中,平面 ∥平面
∥平面 ,
, ⊥平面
⊥平面 ,
, ,
,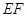 ∥
∥ .
. ,
,  .
.
 平面
平面 ;
; ∥平面
∥平面 ;
; 的余弦值.
的余弦值. 、
、 ,能判定
,能判定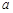

 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,且
,且 ,
, 为
为 中点.
中点.
 平面
平面 的余弦值.
的余弦值. ,给定以下条件:
,给定以下条件: 内不共线的三点到
内不共线的三点到 的距离相等;②
的距离相等;② 是
是 ;
; ;
; 的是( )
的是( ) 中,底面
中,底面 是正方形.已知
是正方形.已知 ,
, .
.
 ;
; .
.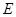 是
是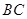 的中点,P点在侧面△SCD内及其边界上运动,并且总是保持
的中点,P点在侧面△SCD内及其边界上运动,并且总是保持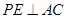 .则动点
.则动点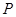 的轨迹与△
的轨迹与△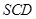 组成的相关图形最有可有是图中的( )
组成的相关图形最有可有是图中的( )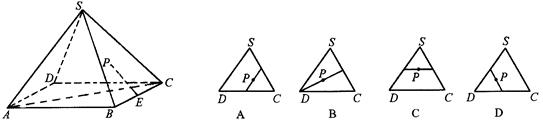
 中,E,F满足
中,E,F满足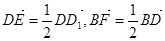 .
.
 ;
; ;
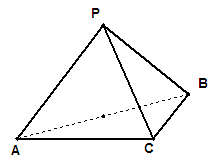
;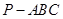 中,
中,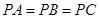 ,
,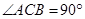 ,
,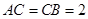 .
. 
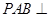 平面
平面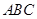 ;
;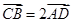 ,且异面直线
,且异面直线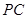 与
与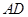 的夹角为
的夹角为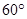 时,求二面角
时,求二面角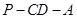 的余弦值.
的余弦值.