题目内容
15.从52张扑克牌(没有大小王)中随机地抽-张牌,这张牌出现下列情形的概率:(1)是7;(2)不是7;(3)是方片;(4)是J或Q或K;(5)既是红心又是草花;(6)比6大比9小;(7)是红色;(8)是红色或黑色.
请设计一种用计算机或计算器模拟上面摸牌试验的方法.
分析 分别求出相应的概率,根据随机数的产生模拟实验即可.
解答 解:有13张红桃,13张梅花,13张方片,13张黑桃,每张牌被抽到的概率均为$\frac{1}{52}$,则
(1)P(是7)=$\frac{4}{52}$=$\frac{1}{13}$;(2)P(不是7)=1-$\frac{1}{13}$=$\frac{12}{13}$;(3)P(是方片)=$\frac{1}{4}$;(4)P(是J或Q或K)=$\frac{3}{13}$;(5)P(既是红心又是草花)=0;
(6)P(比6大比9小)=$\frac{2}{13}$;(7)P(是红色)=$\frac{1}{2}$;(8)P(是红色或黑色)=1,
方法一:把1~52个整数与每张牌对应,再用计算机做模拟实验,
方法二:计算机第1次产生1~4的随机数代表4个花色,
第2次产生的1~13的随机数代表点数.
点评 本题考查了随机数的产生和古典概率的问题,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
6.已知集合M={y|y=2x,x>0},N={x|y=lgx},则M∩N为( )
| A. | (0,+∞) | B. | (1,+∞) | C. | [2,+∞) | D. | [1,+∞) |
10.已知$\frac{(1-i)^{2}}{z}$=1+i(i为虚数单位),则复数z的虚部为( )
| A. | 1 | B. | -1 | C. | -i | D. | i |
20.执行如图所示的程序框图,输出的结果是( )
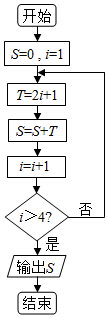

| A. | 15 | B. | 21 | C. | 24 | D. | 35 |
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点