题目内容
2．f（x）=$\frac{1}{3}{x^3}$-$\frac{1}{2}$（a-3）x2-a（2a-3）x+b在（-1，1）上不单调，则实数a的取值范围是（-1，1）∪（1，2）．分析 求出函数的导数，问题转化为f′（x）=（x+a）[x-（2a-3）]=0在（-1，1）有解，得到关于a的不等式，求出a的范围即可．
解答 解：∵$f（x）=\frac{1}{3}{x^3}-\frac{1}{2}（a-3）{x^2}-$a（2a-3）x+b，
∴f′（x）=x2-（a-3）x-a（2a-3），
若f（x）在（-1，1）不单调，
则f′（x）=（x+a）[x-（2a-3）]=0在（-1，1）有解，
故-1＜-a＜1或-1＜2a-3＜1，
解得：-1＜a＜1或1＜a＜2，
故答案为：（-1，1）∪（1，2）．
点评 本题考查了函数的单调性问题，考查导数的应用以及转化思想，是一道中档题．
练习册系列答案
相关题目
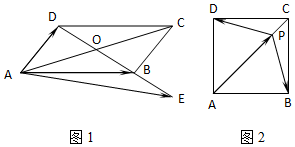（1）如图1，在平行四边形ABCD中，点E是对角线DB的延长线上一点，且OB=BE．记$\overrightarrow{AB}=\overrightarrow a\;，\;\overrightarrow{AD}=\overrightarrow b$，试用向量$\overrightarrow a\;，\;\overrightarrow b$表示$\overrightarrow{AE}$．