题目内容
在 中,角A,B,C的对边分别为a,b,c,若
中,角A,B,C的对边分别为a,b,c,若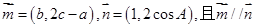 .
.
(1)求B;
(2)设函数 ,求函数
,求函数 上的取值范围.
上的取值范围.
(1) ;(2)
;(2)
解析试题分析:(1)由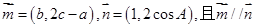 可得
可得 ,然后结合余弦定理求出
,然后结合余弦定理求出 从而确定角B的值.
从而确定角B的值.
(2)结合(1)的结果,利用两角和与差的三角函数公式将函数式化简为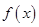

再由 得
得 ,根据正弦函数的性质求得
,根据正弦函数的性质求得 的取值范围.
的取值范围.
解:(1)解法一:
因为 ,所以
,所以  2分
2分
由余弦定理得 ,整理得
,整理得
所以 4分
4分
又因为 ,所以
,所以 . 6分
. 6分
解法二:
因为 ,所以
,所以 2分
2分
由正弦定理得 
所以
整理得
因为 ,所以
,所以 ,所以
,所以 4分
4分
又因为 ,所以
,所以 . 6分
. 6分
(2)


 8分
8分
因为  ,则
,则  , 10分
, 10分
所以  ,
,
即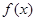 在
在 上取值范围是
上取值范围是 . 12分
. 12分
考点:1、余弦定理;2、两角和与差的三角函数公式;3、正弦函数的性质.

练习册系列答案
相关题目

 写成
写成 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标; 满足
满足 ,且边
,且边 所对的角为
所对的角为 ,试求
,试求 ,且
,且 .
. 的值;
的值;  的值.
的值.  <α<π,0<β<
<α<π,0<β< ,cos(β-α)=
,cos(β-α)= ,求sinβ的值.
,求sinβ的值. 和钝角
和钝角 的终边分别与单位圆交于
的终边分别与单位圆交于 两点.
两点. ,求
,求 的值;
的值; 是单位圆上的一点,且
是单位圆上的一点,且 ,求
,求 和
和 的夹角
的夹角 .
.
 ,
, ,且
,且 ,求
,求 的值.
的值.
 的最小正周期;
的最小正周期; ,
, 的值.
的值.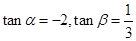 ,其中
,其中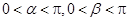 .
.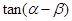 的值;
的值;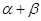 的值.
的值. ,则
,则 等于__________
等于__________