题目内容
已知非零向量
,
同时满足:|
|=|
|和|
+
|=|
-
|,若作
=
,
=
,
=
+
,试判定四边形OACB的形状,并证明.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| OA |
| a |
| OB |
| b |
| OC |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由题意得到方程组解得
⊥
,|
|=|
|,结合
=
+
,从而得到答案.
| a |
| b |
| a |
| b |
| OC |
| a |
| b |
解答:
解:∵
≠
,
≠
,且|
|=|
|和|
+
|=|
-
|,
∴
,解得:
⊥
,|
|=|
|,
作
=
,
=
,
=
+
,
如图示:
 ,
,
∴四边形OACB是正方形,
证明如下:
∵
=
+
,
∴四边形OACB是平行四边形,
又∵
⊥
,|
|=|
|,
∴四边形OACB是正方形.
| a |
| 0 |
| b |
| 0 |
| a |
| b |
| a |
| b |
| a |
| b |
∴
|
| a |
| b |
| a |
| b |
作
| OA |
| a |
| OB |
| b |
| OC |
| a |
| b |
如图示:
 ,
,∴四边形OACB是正方形,
证明如下:
∵
| OC |
| a |
| b |
∴四边形OACB是平行四边形,
又∵
| a |
| b |
| a |
| b |
∴四边形OACB是正方形.
点评:本题考查了平面向量的运算性质及其证明,本题属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设P是?ABCD对角线的交点,O为空间任意一点(不在平面ABCD上),则
+
+
+
等于( )
| OA |
| OB |
| OC |
| OD |
A、4
| ||
B、6
| ||
C、2
| ||
D、
|
若函数f(x)=x3-bx,(b∈R)在区间(1,2)上有零点,则b的取值范围是( )
| A、(4,+∞) |
| B、(1,4) |
| C、(-4,-1) |
| D、(-∞,1) |
 : “方程
: “方程 表示双曲线” (
表示双曲线” ( );命题
);命题 :
: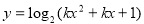 定义域为
定义域为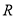 ,若命题
,若命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数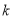 的取值范围.
的取值范围.