题目内容
3.已知函数$f(x)={log_{\frac{1}{2}}}(3+x)+{log_{\frac{1}{2}}}(3-x)$.(Ⅰ) 求f(1)的值;
(Ⅱ) 判断函数f(x)的奇偶性,并加以证明;
(Ⅲ)若f(2x)>0,求实数x的取值范围.
分析 (I)将x=1代入f(x)计算;
(II)先判断定义域是否关于原点对称,再化简f(-x),判断f(-x)与f(x)的关系;
(III)利用函数的单调性和定义域列出不等式组解出.
解答 解:(Ⅰ)f(1)=log${\;}_{\frac{1}{2}}$4+log${\;}_{\frac{1}{2}}$2=-2-1=-3.
(Ⅱ) 函数f(x)是偶函数.
证明:由函数有意义得$\left\{\begin{array}{l}3+x>0\\ 3-x>0\end{array}\right.$,解得-3<x<3,
∴函数f(x)的定义域为{x|-3<x<3}.
∵f(-x)=${log_{\frac{1}{2}}}(3-x)+{log_{\frac{1}{2}}}(3+x)$=f(x),
∴函数$f(x)={log_{\frac{1}{2}}}(3+x)+{log_{\frac{1}{2}}}(3-x)$是偶函数.
(Ⅲ) 由f(2x)>0可得 ${log_{\frac{1}{2}}}(9-{(2x)^2})>{log_{\frac{1}{2}}}1$.
∴$\begin{array}{l}\left\{\begin{array}{l}-3<2x<3\\ 9-{(2x)^2}<1\end{array}\right.\end{array}$,解得$-\frac{3}{2}<x<-\sqrt{2}$,或 $\sqrt{2}<x<\frac{3}{2}$.
∴x的取值范围是(-$\frac{3}{2}$,-$\sqrt{2}$)∪($\sqrt{2}$,$\frac{3}{2}$).
点评 问题考查了对数运算,对数函数的性质,函数单调性的应用,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
11.抛物线y2=2x上与其焦点距离等于3的点的横坐标是( )
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
18.若tan α<0,则( )
| A. | sin α<0 | B. | cos α<0 | C. | sin α•cosα<0 | D. | sin α-cos α<0 |
12.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
(1)请根据上表提供的数据,用最小二乘法求出y关于x的回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{c}$;
(2)已知该厂技改前100吨甲产品的生产能耗为85吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式:$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.$.
| x | 2 | 3 | 4 | 5 |
| y | 1.5 | 2 | 3 | 3.5 |
(2)已知该厂技改前100吨甲产品的生产能耗为85吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式:$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.$.
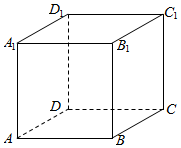 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中.
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中.