题目内容
13.在某次联考数学测试中,学生成绩ξ服从正态分布(100,σ2)(σ>0),若ξ在(80,120)内的概率为0.8,则落在(0,80)内的概率为0.1.分析 根据ξ服从正态分布N(100,σ2),得到曲线的对称轴是直线x=100,利用ξ在(80,120)内取值的概率为0.8,即可求得结论.
解答 解:∵ξ服从正态分布N(100,σ2)
∴曲线的对称轴是直线x=100,
∵ξ在(80,120)内取值的概率为0.8,
∴ξ在(0,100)内取值的概率为0.5,
∴ξ在(0,80)内取值的概率为0.5-0.4=0.1.
故答案为:0.1.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,主要考查正态曲线的对称性,是一个基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.一个几何体的三视图如图,则这个几何体的表面积是( )
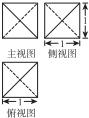

| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{3}$ | D. | $2\sqrt{6}$ |
18.已知x>0,y>0,lg2x+lg8y=lg2,则$\frac{1}{x}+\frac{2}{y}$的最小值是( )
| A. | $7+2\sqrt{6}$ | B. | $4+\sqrt{3}$ | C. | $7+\sqrt{6}$ | D. | $4+2\sqrt{3}$ |
5.下列向量与向量$\overrightarrow{a}$=(-3,4)垂直,且是单位向量的为( )
| A. | (-4,3) | B. | (-3,-4) | C. | (-$\frac{4}{5}$,$\frac{3}{5}$) | D. | (-$\frac{4}{5}$,-$\frac{3}{5}$) |
2.在平面直角坐标系中,以x轴的非负半轴为角的始边,如果角α,β的终边分别与单位圆交于点($\frac{12}{13}$,$\frac{5}{13}$)和(-$\frac{3}{5}$,$\frac{4}{5}$),那么cosαsinβ等于( )
| A. | -$\frac{36}{65}$ | B. | -$\frac{3}{13}$ | C. | $\frac{4}{13}$ | D. | $\frac{48}{65}$ |