题目内容
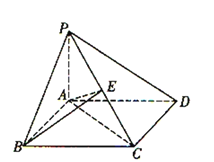
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求证:当
,求证:当![]() 时,
时,![]() ;
;
(2)若函数![]() 在
在![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)![]() 时,求导并判断函数
时,求导并判断函数![]() 的单调性,可得
的单调性,可得![]() 在
在![]() 上单调递增,即当
上单调递增,即当![]() 时,
时,![]() ;
;
(2)构造函数![]() ,求导并判断单调性可得
,求导并判断单调性可得![]() 在
在![]() 上单调递增,可求出
上单调递增,可求出![]() 与
与![]() ,然后分
,然后分![]() 、
、![]() 和
和![]() 三种情况讨论,使得
三种情况讨论,使得![]() 在
在![]() 上单调递减所满足的条件,可求出实数
上单调递减所满足的条件,可求出实数![]() 的取值范围.
的取值范围.
(1)依题意![]() ,定义域为
,定义域为![]() ,
,
![]() .
.
令![]() ,则
,则![]() .
.
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以![]() ,即
,即![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
所以当![]() 时,
时,![]() .
.
(2)设![]() ,则
,则![]() .
.
易知当![]() 时,
时,![]() ,即
,即![]() ,故
,故![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() ,
,![]() .
.
①若![]() ,则在
,则在![]() 上,
上,![]() ,所以
,所以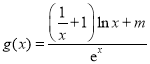 .
.
所以![]() .
.
令![]() .
.
在![]() 上,要使
上,要使![]() 单调递减,则
单调递减,则![]() ,从而
,从而![]() .
.
因为![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
所以![]() ,所以
,所以![]() .
.
②若![]() ,即
,即![]() ,则在
,则在![]() 上,
上,![]() ,
,
所以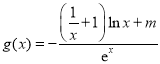 ,由①可知
,由①可知![]() .
.
所以当![]() 时,
时,![]() ,
,
从而![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
③若![]() ,则存在
,则存在![]() ,使得
,使得![]() ,从而
,从而![]() .
.
而![]() ,
,![]() ,从而
,从而![]() 在区间
在区间![]() 上不单调递减.
上不单调递减.
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某公司为了了解年研发资金投人量![]() (单位:亿元)对年销售额
(单位:亿元)对年销售额![]() (单位:亿元)的影响.对公司近
(单位:亿元)的影响.对公司近![]() 年的年研发资金投入量
年的年研发资金投入量![]() 和年销售额
和年销售额![]() 的数据,进行了对比分析,建立了两个函数模型:①
的数据,进行了对比分析,建立了两个函数模型:①![]() ,②
,②![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 均为常数,
均为常数,![]() 为自然对数的底数.并得到一些统计量的值.令
为自然对数的底数.并得到一些统计量的值.令![]() ,
,![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)(ⅰ)根据(1)的选择及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(ⅱ)若下一年销售额![]() 需达到
需达到![]() 亿元,预测下一年的研发资金投入量
亿元,预测下一年的研发资金投入量![]() 是多少亿元?
是多少亿元?
附:①相关系数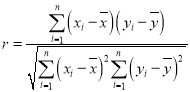 ,
,
回归直线![]() 中公式分别为:
中公式分别为: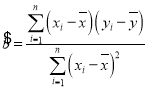 ,
,![]() ;
;
②参考数据:![]() ,
,![]() ,
,![]() .
.