题目内容
【题目】已知数列![]() ,
,![]() 满足
满足![]() (
(![]() …).
…).
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 且
且![]() ,则数列
,则数列![]() 中第几项最小?请说明理由;
中第几项最小?请说明理由;
(3)若![]() (n=1,2,3,…),求证:“数列
(n=1,2,3,…),求证:“数列![]() 为等差数列”的充分必要条件是“数列
为等差数列”的充分必要条件是“数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)”.
(n=1,2,3,…)”.
【答案】(1)![]() (2)第8项最小,理由见解析(3)证明见解析
(2)第8项最小,理由见解析(3)证明见解析
【解析】
(1)由![]() 可判断
可判断![]() 是等差数列,则
是等差数列,则![]()
![]() ,进而利用等差数列性质求解即可;
,进而利用等差数列性质求解即可;
(2)法一:利用数列的增减性进行判断即可;
法二:求出![]() 的通项公式,利用均值不等式求最值,即可得到取等条件,进而求解;
的通项公式,利用均值不等式求最值,即可得到取等条件,进而求解;
(3)若数列![]() 为等差数列,设其公差为
为等差数列,设其公差为![]() ,说明数列
,说明数列![]() 为等差数列,由
为等差数列,由![]() (
(![]() …)推出
…)推出![]() (
(![]() …);若数列
…);若数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…),设公差为
(n=1,2,3,…),设公差为![]() ,转化推出
,转化推出![]() (
(![]() …),说明数列
…),说明数列![]() 为等差数列,结论得证
为等差数列,结论得证
(1)由![]() ,可得
,可得![]() ,故
,故![]() 是等差数列,
是等差数列,
所以![]()
![]()
(2)![]()
![]()
当![]() 时,则
时,则![]() ,解得
,解得![]() ,
,
当![]() 时,则
时,则![]() ,解得
,解得![]() ,
,
故有![]() ,
,
所以数列![]() 中
中![]() 最小,即第8项最小
最小,即第8项最小
法二:由![]() ,
,
可知![]()
![]()
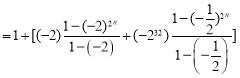
![]()
![]() (当且仅当
(当且仅当![]() ,即
,即![]() 时取等号)
时取等号)
所以数列![]() 中的第8项最小
中的第8项最小
(3)证明:若数列![]() 为等差数列,设其公差为
为等差数列,设其公差为![]() ,
,
则![]() 为常数,
为常数,
所以数列![]() 为等差数列,
为等差数列,
由![]() (
(![]() …),
…),
则![]() ,故
,故![]() (
(![]() …)成立,故必要性成立;
…)成立,故必要性成立;
若数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…),设
(n=1,2,3,…),设![]() 的公差为
的公差为![]() ,
,
则![]() (n=1,2,3,…),
(n=1,2,3,…),
又![]() ,故
,故![]() ,
,
又![]() ,
,![]() ,故
,故![]() ,
,
所以![]()
![]() ,故有
,故有![]() ,所以
,所以![]() 为常数,
为常数,
故数列![]() 为等差数列,故充分性成立,
为等差数列,故充分性成立,
综上可得,“数列![]() 为等差数列”的充分必要条件是“数列
为等差数列”的充分必要条件是“数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)”
(n=1,2,3,…)”

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】空气质量指数![]() 是反映空气质量状况的指数,
是反映空气质量状况的指数,![]() 指数值越小,表明空气质量越好,其对应关系如表:
指数值越小,表明空气质量越好,其对应关系如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市10月1日—20日![]() 指数变化趋势:
指数变化趋势:
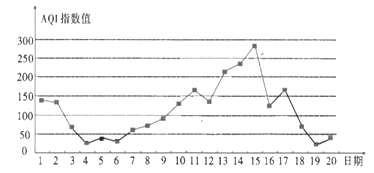
下列叙述正确的是( )
A.该市10月的前半个月的空气质量越来越好
B.这20天中的中度污染及以上的天数占![]()
C.这20天中![]() 指数值的中位数略高于100
指数值的中位数略高于100
D.总体来说,该市10月上旬的空气质量比中旬的空气质量差