题目内容
4.在△ABC中,已知角A,B,C所对的边是a,b,c,则下列说法正确的有②③⑤(写出所有正确命题的编号).①若$a=2,b=2\sqrt{3},A=30°$,则B=60°
②若sinA>sinB,则a>b,反之也成立
③若A=60°且$\overrightarrow{AC}•\overrightarrow{AB}=2$,则△ABC的面积是$\sqrt{3}$
④若b2=ac且$cos(A-C)=\frac{3}{2}-cosB$,则$B=\frac{π}{3}或B=\frac{2π}{3}$
⑤若c2sin2B+b2sin2C=2bccosBcosC,则△ABC一定是直角三角形.
分析 利用正弦定理进行分析判断.
解答 解:对于①,由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,∴sinB=$\frac{bsinA}{a}=\frac{\sqrt{3}}{2}$,
∴B=60°或B=120°,故①错误.
对于②,由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$得$\frac{a}{b}=\frac{sinA}{sinB}$,故②正确.
对于③,∵$\overrightarrow{AC}•\overrightarrow{AB}$=bccosA=2,∴bc=4,
∴S=$\frac{1}{2}bcsinA$=$\frac{1}{2}×4×\frac{\sqrt{3}}{2}=\sqrt{3}$,故③正确.
对于④,∵$cos(A-C)=\frac{3}{2}-cosB$=$\frac{3}{2}+cos(A+C)$,
∴cosAcosC+sinAsinC=$\frac{3}{2}$+cosAcosC-sinAsinC,
∴sinAsinC=$\frac{3}{4}$.
∵b2=ac,∴sin2B=sinAsinC=$\frac{3}{4}$,
∴sinB=$\frac{\sqrt{3}}{2}$,∴B=$\frac{π}{3}$或B=$\frac{2π}{3}$.
若B=$\frac{2π}{3}$,则cos(A-C)=$\frac{3}{2}$-cosB=$\frac{3}{2}$+$\frac{1}{2}$=2>1,故④错误.
对于⑤,∵c2sin2B+b2sin2C=2bccosBcosC,
∴sin2Csin2B+sin2Bsin2C=2sinBsinCcosBcosC,
∴sinBsinC=cosBcosC,∴cosBcosC-sinBsinC=0,
∴cosA=0,即A=90°.故⑤正确.
故答案为:②③⑤.
点评 本题考查了正弦定理的应用,属于中档题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案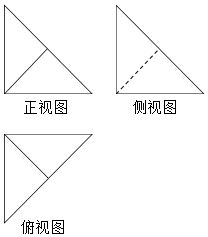 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
| A. | 2 | B. | $\frac{\sqrt{2}}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
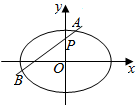 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为4.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为4.