题目内容
14.若cos2x=1,x∈R,x={x|x=kπ,k∈Z}.分析 根据题意求出cosx的值,再利用余弦函数的图象与性质求出x的取值范围即可.
解答 解:∵cos2x=1,
∴cosx=±1,
当cosx=1时,x=2kπ,k∈Z,
当cosx=-1时,x=π+2kπ,k∈Z;
综上,该方程的解为{x|x=kπ,k∈Z}.
故答案为:{x|x=kπ,k∈Z}.
点评 本题主要考查了余弦函数的图象与性质的应用问题,是基础知识的灵活运用问题.

练习册系列答案
相关题目
2.多次执行如图所示的程序框图,输出的$\frac{m}{n}$的值会稳定在某个常数附近,则这个常数为( )
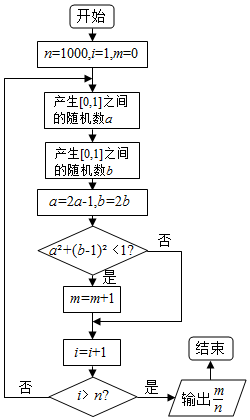

| A. | $\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{16}$ |
19.已知各项均为正数的数列{an},其前n项和为Sn,且Sn,an,$\frac{1}{2}$成等差数列,则数列{an}的通项公式为( )
| A. | 2n-3 | B. | 2n-2 | C. | 2n-1 | D. | 2n-2+1 |
6.执行如图的程序框图,若输入M的值为1,则输出的S=( )


| A. | 6 | B. | 12 | C. | 14 | D. | 20 |
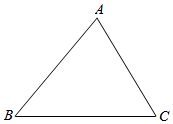 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,已知A=60°,a=3.求△ABC的周长L的最大值.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,已知A=60°,a=3.求△ABC的周长L的最大值.