题目内容
13.已知t>0,函数f(x)=2x-1+$\sqrt{4+t-2tx}$的最大值为g(t),则g(t)的最小值为( )| A. | 2 | B. | $\frac{\sqrt{2}}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
分析 令$\sqrt{4+t-2tx}$=m,则2x-1=$\frac{4-{m}^{2}}{t}$,从而利用配方法求最大值,再由基本不等式求最小值即可.
解答 解:令$\sqrt{4+t-2tx}$=m,则2x-1=$\frac{4-{m}^{2}}{t}$,
故f(x)=2x-1+$\sqrt{4+t-2tx}$
=$\frac{4-{m}^{2}}{t}$+m=$\frac{-(m-\frac{t}{2})^{2}+4+\frac{{t}^{2}}{4}}{t}$=F(m),
故g(t)=Fmax(m)=$\frac{4}{t}$+$\frac{t}{4}$≥2,
(当且仅当t=4时,等号成立),
故选A.
点评 本题考查了配方法的应用及基本不等式的应用,同时考查了换元法的应用.

练习册系列答案
相关题目
3.已知△ABC中,$AB=\sqrt{3},AC=1$,且B=30°,则角C的大小为( )
| A. | 60°或120° | B. | 120° | C. | 60° | D. | 30° |
1.在直角坐标系xOy中,已知点A(0,1),点B(-3,4),若点C在∠AOB的平分线上,则向量$\overrightarrow{OC}$可以等于( )
| A. | (-2,3) | B. | (-2,4) | C. | (-1,4) | D. | (-1,3) |
8.执行如图所示的程序框图,输出S的值是( )
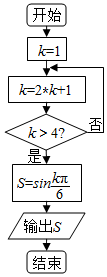

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
2.多次执行如图所示的程序框图,输出的$\frac{m}{n}$的值会稳定在某个常数附近,则这个常数为( )
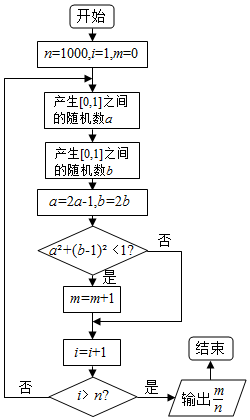

| A. | $\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{16}$ |