题目内容
12.表面积为16π的球面上有四个点P,A,B,C,且△ABC是边长为$2\sqrt{3}$的等边三角形,若平面PAB⊥平面ABC,则棱锥P-ABC体积的最大值为3.分析 取AB中点N,由题设条件推导出当棱锥P-ABC体积取最大值时,PN⊥AB,PN⊥平面ABC,由此能求出结果.
解答 解:由题意知半径为2的球面上,AB=BC=CA=2$\sqrt{3}$,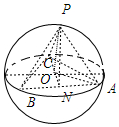
△ABC是大圆上的三角形,
设圆为O,AB中点为N,则ON=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,
∵平面PAB⊥平面ABC,
∴棱锥P-ABC体积取最大值时,PN⊥AB,PN⊥平面ABC,
∴PN=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴棱锥P-ABC体积的最大值为:
$V=\frac{1}{3}×\frac{\sqrt{3}}{4}×(2\sqrt{3})^{2}×\sqrt{3}$=3.
故答案为:3.
点评 本题考查三棱锥的体积的最大值的求法,考查球的性质,探索向何体的位置情况,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
相关题目
20.已知集合A={-1,0,1},B={x|x2<1},则A∩B=( )
| A. | ∅ | B. | {0} | C. | {-1,1} | D. | {-1,0,1} |
17.已知关于x的方程$\frac{1}{x+2}=a|x|$有三个不同的实数解,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,1) | C. | (1,+∞) | D. | (0,+∞) |
4.已知直线x-y+1=0与双曲线$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{b}$=1(ab<0)相交于P,Q两点,且OP⊥OQ(O为坐标原点),则$\frac{1}{a}+\frac{1}{b}$=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |