题目内容
13．若a＞$\frac{\sqrt{5}-1}{2}$，a≠1，x=|loga2|，y=loga+12，z=loga+22，则（ ）| A． | x＞y＞z | B． | z＞y＞x | C． | y＞z＞x | D． | x＞z＞y |
分析 由a＞$\frac{\sqrt{5}-1}{2}$，不妨令a=2，进而求出x，y，z的值（或范围），可得答案．
解答 解：∵a＞$\frac{\sqrt{5}-1}{2}$，
不妨令a=2，
则x=|log22|=1，
y=log32∈（$\frac{1}{2}$，1），
z=log42=$\frac{1}{2}$，
∴x＞y＞z，
故选：A．
点评 本题考查的知识点是对数值的大小比较，对数运算，由于本题是选择题，故可采用特值代入法进而判断．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
1．已知m＞0，且10x=lg10m+lg$\frac{1}{m}$，则x的值为（ ）
| A． | 2 | B． | 1 | C． | 0 | D． | -1 |
1．
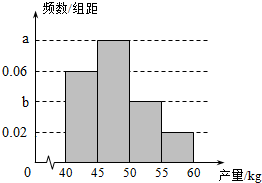果农种了一片果树，收获时，果农随机随机选取果树20株作为样本．测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，45]，（45，50]，（50，55]，（55，60]，进行分组，得到频率分布直方图如图，已知样本中产量在区间（45，50]上的果树株数是产量在区间（50，60]上的果树株数的$\frac{4}{3}$倍．
（1）求a，b的值；
（2）果树的价格如下表：
若果农从这20株样本中随机抽取两株以总价400元卖出，求果农获利的分布和期望．
果农种了一片果树，收获时，果农随机随机选取果树20株作为样本．测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，45]，（45，50]，（50，55]，（55，60]，进行分组，得到频率分布直方图如图，已知样本中产量在区间（45，50]上的果树株数是产量在区间（50，60]上的果树株数的$\frac{4}{3}$倍．（1）求a，b的值；
（2）果树的价格如下表：
| 产量 | （40，45] | （45，50] | （50，55] | （55，60] |
| 价格（百元/棵） | 1 | 2 | 3 | 4 |