设集合M={y|y=x2}.N={x|y=$\sqrt{{x}^{2}+2x+1}$}.则M∩N为( )A．M?NB．M?NC．M=ND．M∩N=∅ 题目和参考答案——青夏教育精英家教网—

题目内容

6．设集合M={y|y=x²}，N={x|y=$\sqrt{{x}^{2}+2x+1}$}，则M∩N为（　　）

A．

M?N

B．

M?N

C．

M=N

D．

M∩N=∅

分析求出M中y的范围确定出M，求出N中x的范围确定出N，找出两集合的交集即可．

解答解：由M中y=x²≥0，得到M=[0，+∞），
由N中y=$\sqrt{{x}^{2}+2x+1}$，得到x²+2x+1≥0，即（x+1）²≥0，
解得：x∈R，即B=R，
则M?N，
故选：A．

点评此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案

8．已知向量$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$不共线，x，y∈R，且有（3x-4y）$\overrightarrow{{e}_{1}}$+（2x-3y）$\overrightarrow{{e}_{2}}$=6$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$，则x-y的值为（　　）

14．已知函数f（x）对任意实数x均有f（x）=kf（x+2），其中常数k为负数，且f（x）在区间[0，2]有表达式f（x）=x（x-2）
（I）求出f（-1），f（2.5）的值；
（Ⅱ）若函数f（x）在区间[-2，2]的最大值与最小值分别为m，n，且m-n=3，求k的值．

1．在△ABC中，AB=5，BC=7，AC=8，则$\overrightarrow{BA}$•$\overrightarrow{BC}$的值为（　　）

11．设函数f（x）=$\frac{1}{1+x}$，g（x）=x²+2，则f[g（2）]=（　　）

18．

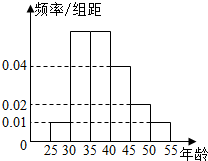为响应工业园区举行的万人体质监测活动，某高校招募了N名志愿服务者，将所有志愿者按年龄情况分为25～30，30～35，35～40，45～50，50～55六个层次，其频率分布直方图如图所示，已知35～45之间的志愿者共20人．
（1）计算N的值；
（2）从45～55之间的志愿者（其中共有4名女教师，其余全为男教师）中随机选取2名担任后勤保障工作，求恰好抽到1名女教师，1名男教师的概率．

15．请观察数列：1，1，2，3，5，（　　），13…运用合情推理，括号里的数最可能是（　　）

16．求值：
（Ⅰ）${log_3}\sqrt{27}+lg25+lg4+{7^{{{log}_7}2}}+lg1$；
（Ⅱ）0.027${\;}^{-\frac{1}{3}}$-（-$\frac{1}{6}$）^-2+81^0.75+（$\frac{1}{9}$）⁰-3^-1．

试题分类