题目内容
如图,三棱锥SABC中,SC丄底面ABC,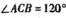 ,
,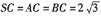 ,M
,M 为SB中点,N在AB上,满足
为SB中点,N在AB上,满足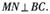
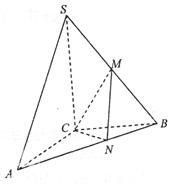
(I)求点N到平面SBC的距离;
(II)求二面角C-MN-B的大小.
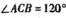 ,
,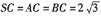 ,M
,M 为SB中点,N在AB上,满足
为SB中点,N在AB上,满足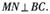

(I)求点N到平面SBC的距离;
(II)求二面角C-MN-B的大小.
19.(12分)
解:(1)取 的中点
的中点 ,连结
,连结 、
、 ,则由
,则由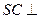 底面
底面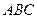 ,
,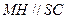 ,知
,知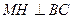 ,又
,又 ,∴
,∴ 平面
平面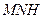 ,∴
,∴ ,∴
,∴ 平面SBC,∴
平面SBC,∴ 即为点N到平面SBC的距离.
即为点N到平面SBC的距离.
由题易知 ,所以
,所以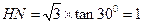 .…………5分
.…………5分
(2)(方法一)在直角三角形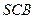 中,因为
中,因为 为
为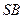 的中点,所以
的中点,所以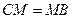 。由(1)知
。由(1)知 ,所以
,所以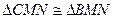 ,作
,作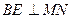 于点
于点 ,连结
,连结 ,则
,则 ,所
,所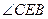 为二面角
为二面角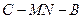 的平面角.
的平面角.
在三角形 中,易知
中,易知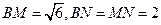 ,故可求
,故可求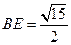 ,所以
,所以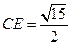 ,在
,在 中,由余弦定理可得
中,由余弦定理可得 ,所以
,所以 ,即二面角
,即二面角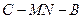 的大小为
的大小为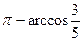 . …………12分
. …………12分
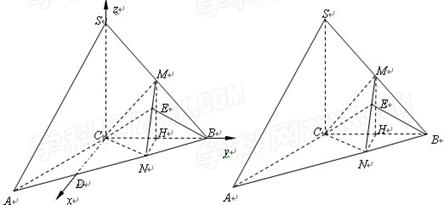
(方法二)过C作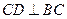 交AB于D,如图建立空间直角坐标系,则易知点
交AB于D,如图建立空间直角坐标系,则易知点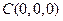 、
、 、
、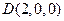 、
、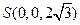 、
、 、
、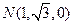 ,则
,则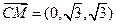 、
、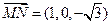 、
、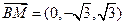 ,
,
设平面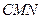 的法向量为
的法向量为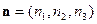 ,则由
,则由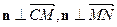 ,得
,得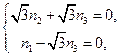 故可取
故可取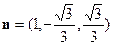 ,
,
再设平面 的法向量为
的法向量为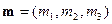 ,则由
,则由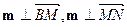 ,得
,得 故可取
故可取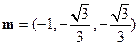 ,则向量
,则向量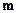 与
与
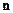 的夹角大小即为二面角
的夹角大小即为二面角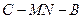 的大小。
的大小。
 ,故二面角
,故二面角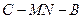 的大小
的大小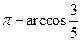 …………12分
…………12分
解:(1)取
 的中点
的中点 ,连结
,连结 、
、 ,则由
,则由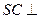 底面
底面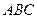 ,
,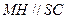 ,知
,知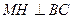 ,又
,又 ,∴
,∴ 平面
平面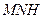 ,∴
,∴ ,∴
,∴ 平面SBC,∴
平面SBC,∴ 即为点N到平面SBC的距离.
即为点N到平面SBC的距离.由题易知
 ,所以
,所以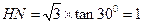 .…………5分
.…………5分(2)(方法一)在直角三角形
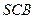 中,因为
中,因为 为
为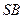 的中点,所以
的中点,所以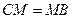 。由(1)知
。由(1)知 ,所以
,所以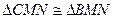 ,作
,作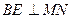 于点
于点 ,连结
,连结 ,则
,则 ,所
,所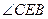 为二面角
为二面角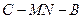 的平面角.
的平面角.在三角形
 中,易知
中,易知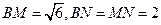 ,故可求
,故可求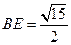 ,所以
,所以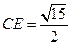 ,在
,在 中,由余弦定理可得
中,由余弦定理可得 ,所以
,所以 ,即二面角
,即二面角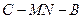 的大小为
的大小为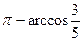 . …………12分
. …………12分
(方法二)过C作
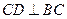 交AB于D,如图建立空间直角坐标系,则易知点
交AB于D,如图建立空间直角坐标系,则易知点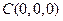 、
、 、
、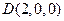 、
、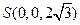 、
、 、
、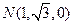 ,则
,则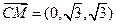 、
、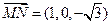 、
、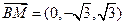 ,
, 设平面
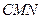 的法向量为
的法向量为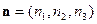 ,则由
,则由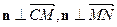 ,得
,得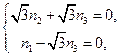 故可取
故可取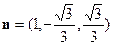 ,
,再设平面
 的法向量为
的法向量为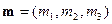 ,则由
,则由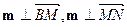 ,得
,得 故可取
故可取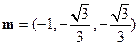 ,则向量
,则向量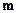 与
与
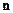 的夹角大小即为二面角
的夹角大小即为二面角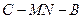 的大小。
的大小。 ,故二面角
,故二面角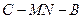 的大小
的大小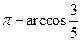 …………12分
…………12分略

练习册系列答案
相关题目
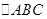 所在平面互相垂直,F为BC的中点,
所在平面互相垂直,F为BC的中点,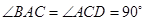 ,AE∥CD,
,AE∥CD,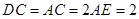 .
.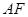 ∥平面
∥平面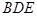 ;
;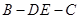 的余弦值.
的余弦值.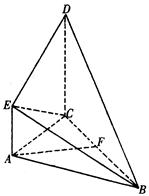
 ,AA1=4,点D是AB的中点
,AA1=4,点D是AB的中点 AC⊥BC1;
AC⊥BC1;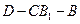 的平面角的正切值.
的平面角的正切值.
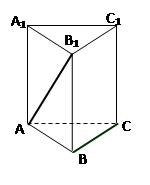


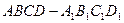 中,E是BC的中点,M、N分别是AE、
中,E是BC的中点,M、N分别是AE、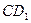 的中点,
的中点,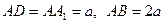 .
. 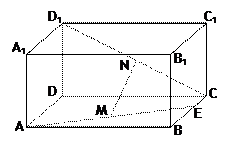
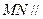 平面
平面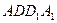
 ,则
,则 =_____.
=_____.

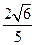

 在平面
在平面 内,
内, ,
, 是
是 ,则点
,则点 在
在 上
上 上
上 上
上