题目内容
(10分)
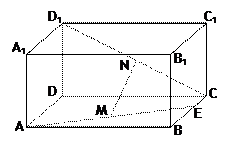
长方体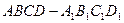 中,E是BC的中点,M、N分别是AE、
中,E是BC的中点,M、N分别是AE、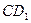 的中点,
的中点,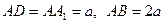 .
.
(1) 求证: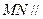 平面
平面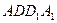
(2)求异面直线AE与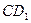 所成角的余弦值
所成角的余弦值
长方体
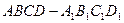 中,E是BC的中点,M、N分别是AE、
中,E是BC的中点,M、N分别是AE、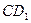 的中点,
的中点,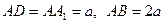 .
. 
(1) 求证:
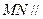 平面
平面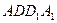
(2)求异面直线AE与
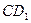 所成角的余弦值
所成角的余弦值(1)证明:取CD的中点
 K,连接MK、NK
K,连接MK、NK 分别是AE、
分别是AE、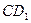 、CD的中点
、CD的中点



(2)取
 的中点F,连接EF、AF,则
的中点F,连接EF、AF,则

 四边形
四边形 是平行四边形
是平行四边形
 (或其补角)是异面直线AE和
(或其补角)是异面直线AE和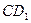 所成的角
所成的角在
 中,易得:
中,易得: ,
, ,
,
由余弦定理得:

故:异面直线AE与
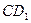 所成角的余弦值为
所成角的余弦值为 。
。略

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
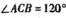 ,
,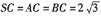 ,M
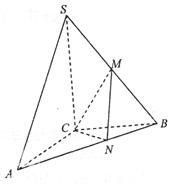
,M 为SB中点,N在AB上,满足
为SB中点,N在AB上,满足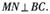
 中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).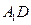 与直线
与直线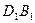 所成的角为 ▲ .
所成的角为 ▲ .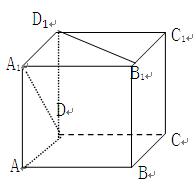
 为异面直线,直线c∥a,则c与b的位置关系是 ( )
为异面直线,直线c∥a,则c与b的位置关系是 ( ) 平行
平行 B1C上的点M满足B1M=λB1C,若向量AD与BM的夹角小于45º,求实数λ的取值范围
B1C上的点M满足B1M=λB1C,若向量AD与BM的夹角小于45º,求实数λ的取值范围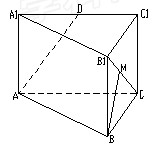
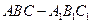 中,
中,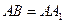 ,则
,则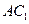 与平面
与平面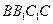 所成角的正弦值等于( )
所成角的正弦值等于( )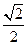
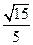
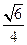
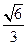
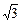 a、
a、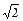 a,其余四根均为a,用它们搭成三棱锥,则其中两条较长的棱所在的直线的夹角的余弦值为 ( )
a,其余四根均为a,用它们搭成三棱锥,则其中两条较长的棱所在的直线的夹角的余弦值为 ( )