题目内容

当点（x，y）在函数y=- $数学公式$ x+ $数学公式$ 上移动时，z=3^x+27^y+1的最小值是

A.
3 $数学公式$
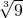
B.
7
C.
1+2 $数学公式$
D.
6

B
分析：先分析基本不等式的条件，再利用基本不等式及点（x，y）在函数y=- $\text{[math]}$ x+ $\text{[math]}$ 上移动，即可求得z=3^x+27^y+1的最小值．
解答：∵3^x＞0，27^y＞0
∴z=3^x+27^y+1≥2 $\text{[math]}$ = $\text{[math]}$
∵点（x，y）在函数y=- $\text{[math]}$ x+ $\text{[math]}$ 上移动
∴x+3y=2
∴ $\text{[math]}$ ，当且仅当x=3y，即 $\text{[math]}$ 时，取等号．
∴3^x+27^y+1≥7，即z=3^x+27^y+1的最小值是7
故选B．
点评：本题考查运用基本不等式求函数的最值，明确基本不等式的使用条件：一正二定三相等是解题的关键．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

己知f（x）=log₂（x+1），当点（x，y）在函数y=f（x）的图象上时，点(

)在函数y=g（x）的图象上．
（1）写出y=g（x）的解析式；
（2）求f（x）-g（x）=0方程的根．

己知f（x）=log₂（x+1），当点（x，y）在函数y=f（x）的图象上时，点（-x，-y）在函数y=g（x）的图象上．
（1）写出y=g（x）的解析式；
（2）求方程f（x）+2g（x）=0的根．

已知函数f（x）=log₂（x+1）．当点（x，y）在函数y=f（x）的图象上运动时，点（

）在函数y=g（x）（x＞-

）的图象上运动．
（1）求函数y=g（x）的解析式；
（2）求函数F（x）=f（x）-g（x）的零点．
（3）函数F（x）在x∈（0，1）上是否有最大值、最小值；若有，求出最大值、最小值；若没有请说明理由．

当点（x，y）在函数y=-

上移动时，z=3^x+27^y+1的最小值是（　　）

3	9

已知f（x）=log₂（x+1），当点（x，y）在函数y=f（x）的图象上运动时，点(

)在函数y=g（x）的图象上运动．
（1）求函数y=g（x）的解析式．
（2）求使g（x）＞f（x）的x的取值范围．
（3）在（2）的范围内，求y=g（x）-f（x）的最大值．