题目内容
已知△ABC的顶点B、C在椭圆
+
=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是 .
| x2 |
| 4 |
| y3 |
| 3 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据椭圆的定义即知△ABC的周长为4a=8.
解答:
8解:如图,由椭圆的标准方程知a=2;

根据椭圆的定义知,△ABC的周长为4a=8.
故答案为:8.

根据椭圆的定义知,△ABC的周长为4a=8.
故答案为:8.
点评:考查椭圆的标准方程,椭圆的焦点,以及椭圆的定义.

练习册系列答案
相关题目
圆柱的轴截面(经过圆柱的轴所作的截面)是边长为5cm的正方形ABCD,则圆柱侧面上从A到C的最短距离为( )
| A、10 cm | ||||
B、
| ||||
C、5
| ||||
D、5
|
已知椭圆
+
=1(a>b>0)的左顶点为A,左焦点为F,上顶点为B,且∠BAO+∠BFO=90°(O为坐标原点),则椭圆的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,正方体ABCD-A1B1C1D1中,AB=2,则三棱锥A-A1B1C的体积是
如图,正方体ABCD-A1B1C1D1中,AB=2,则三棱锥A-A1B1C的体积是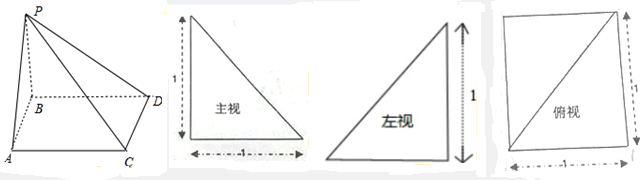 (1)求四棱锥的体积和表面积;
(1)求四棱锥的体积和表面积;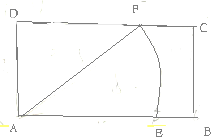 如图,矩形ABCD两邻边长分别为AB=6,AD=3,以A为圆心,5为半径画圆交AB于E,交CD于F,定义点集I={P|AP≤5}
如图,矩形ABCD两邻边长分别为AB=6,AD=3,以A为圆心,5为半径画圆交AB于E,交CD于F,定义点集I={P|AP≤5}