题目内容

求函数y=-（sinx）3-2sinx的最小值．
考点：函数的最值及其几何意义
专题：计算题,函数的性质及应用
分析：换元，确定函数的单调性，即可求出函数的最小值．
解答： 解：令t=sinx（-1≤t≤1），则y=-t3-2t，
∴y′=-3t2-2＜0，
∴函数在[-1，1]上单调递减，
∴t=1时，函数y=-（sinx）3-2sinx的最小值为-3．
点评：本题考查函数的最小值，考查学生的计算能力，确定函数的单调性是关键．
练习册系列答案
相关题目
设函数f（x）=4-ax，g（x）=4-logbx，h（x）=4-xe的图象都经过点p（
1
2
，2），若函数f（x），g（x），h（x）的零点分别为x1，x2，x3，则x1+x2+x3=（　　）
A、
7
6
B、
6
5
C、
5
4
D、
3
2
已知数列{an}是公差为-2的等差数列，a6是a1+2与a3的等比中项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列{an}的前n项和为Sn，求Sn的最大值．
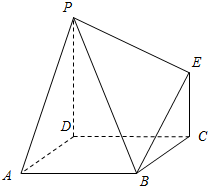如图，简单组合体ABCDPE，其底面ABCD是边长为2的正方形，PD⊥平面ABCD，EC∥PD，且PD=2EC=2．
（1）在线段PB上找一点M，使得ME⊥平面PBD；
（2）求平面PBE与平面PAB的夹角．
已知函数f（x）=x2-（2a-4）x+2在[-1，1]内的最小值为g（a），求g（a）的最大值．
已知函数f（x）=
1
3
x3-x2
（1）求f（x）在R上的极值；
（2）已知a∈R，若g（x）=f（x）+ax，讨论g（x）的单调性．
数列{an}的前n项和为Sn=n（n+1），正项数列{bn}满足bn+2=
bn+12
bn
，且b1b3=4，b4=8．
（1）求数列{an}，{bn}的通项；
（2）数列{cn}满足cn=
S2n
4bn
，若c1c2…cn取得最大值时，求n的值．
已知数列{an}为公差不为0的等差数列，a5和a7的等差中项为6，且a2，a4，a8成等比数列，令bn=
1
an•an+1
，数列{bn}的前n项和为Tn．
（Ⅰ）求an及Tn；
（Ⅱ）若Tn≤λan+1，对?n∈N*恒成立，求实数λ的最小值．
已知Sn为数列{an}的前n项和，且a2+S2=31，an+1=3an-2n（n∈N*）．
（Ⅰ）求证：{an-2n}为等比数列；
（Ⅱ）求数列{an}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网