题目内容
函数 =
= 的值域是 ( )
的值域是 ( )
 =
= 的值域是 ( )
的值域是 ( )| A.[-1,1] | B.(-1,1] | C.[-1,1) | D.(-1,1) |
B
 ,根据复合函数的单调性判断原则可得,当
,根据复合函数的单调性判断原则可得,当 时,
时, 单调增,则
单调增,则 单调减,此时
单调减,此时 ,当
,当 时,
时, 单调减,则
单调减,则 单调增,此时
单调增,此时 。综上可得,
。综上可得, ,故选B
,故选B
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
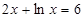 的解为
的解为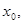 则
则 所在的区间是( )
所在的区间是( )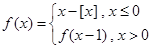 ,其中
,其中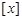 表示不超过
表示不超过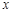 的最大整数,如:
的最大整数,如: 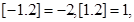
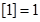 . 则(i)
. 则(i) ;
;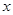 的方程
的方程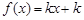 有三个不同的根,则实数
有三个不同的根,则实数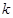 的取值范围是.
的取值范围是.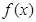 是定义在
是定义在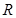 上的奇函数,且当
上的奇函数,且当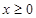 时,
时,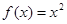 . 若对任意的
. 若对任意的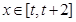 ,不等式
,不等式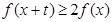 恒成立,则实数
恒成立,则实数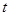 的取值范围是 ( ▲ )
的取值范围是 ( ▲ )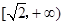
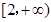
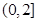
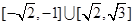
 的图象关于点
的图象关于点 对称,且函数
对称,且函数 为奇函数,则下列结论:(1)点
为奇函数,则下列结论:(1)点 ;(2)当
;(2)当 时,
时, 恒成立;(3)关于
恒成立;(3)关于 的方程
的方程 有且只有两个实根。其中正确结论的题号为( )
有且只有两个实根。其中正确结论的题号为( ) 上的函数
上的函数 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 称为函数
称为函数 .
. 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上的有界函数,且
上的有界函数,且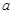 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界
上的上界 的取值范围.
的取值范围. ,当点
,当点 是函数
是函数 图象上的点
图象上的点 时,点
时,点 是函数
是函数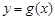 图象上的点.
图象上的点. 时,恒有
时,恒有 ,试确定
,试确定 的取值范围;
的取值范围; 个单位得到
个单位得到 的图象,函数
的图象,函数
 ,(
,( )在
)在 的最大值为
的最大值为 ,求
,求 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为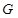 函数.
函数. ,总有
,总有 ;
; 时,总有
时,总有 成立.
成立. 与
与 是定义在
是定义在 是否为
是否为 函数?并说明理由;
函数?并说明理由; 是
是 的值;
的值; ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 , 深为3 m。如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?
, 深为3 m。如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?