题目内容
..(本小题满分14分)定义在 上的函数
上的函数 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.已知函数
的上界.已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若 是
是 上的有界函数,且
上的有界函数,且 的上界为3,求实数
的上界为3,求实数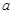 的取值范围;
的取值范围;
(Ⅲ)若 ,求函数
,求函数 在
在 上的上界
上的上界 的取值范围.
的取值范围.
 上的函数
上的函数 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.已知函数
的上界.已知函数 .
.(Ⅰ)当
 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;(Ⅱ)若
 是
是 上的有界函数,且
上的有界函数,且 的上界为3,求实数
的上界为3,求实数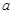 的取值范围;
的取值范围;(Ⅲ)若
 ,求函数
,求函数 在
在 上的上界
上的上界 的取值范围.
的取值范围.解:(Ⅰ)当
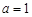 时,
时,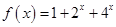 .
.∵
 在
在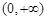 上递增,所以
上递增,所以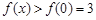 ,
,即
 在
在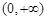 上的值域为
上的值域为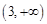 . …………………………… 2分
. …………………………… 2分故不存在常数
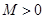 ,使
,使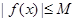 成立.
成立. 所以函数
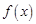 在
在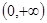 上不是有界函数.………………………… 4分
上不是有界函数.………………………… 4分(Ⅱ)∵函数
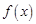 在
在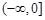 上是以3为上界的有界函数,
上是以3为上界的有界函数,
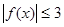 在
在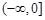 上恒成立.
上恒成立. 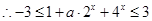 ,
, 在
在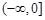 上恒成立.
上恒成立.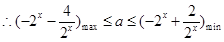 …………………………………… 6分
…………………………………… 6分设
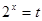 ,
,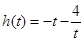 ,
,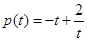 .
.由
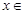
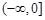 ,得
,得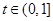 .设
.设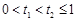 ,则
,则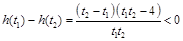 ,
,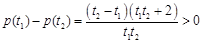 ,
,所以
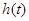 在
在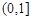 上递增,
上递增,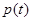 在
在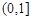 上递减.
上递减.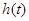 在
在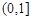 上的最大值为
上的最大值为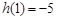 ,
,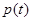 在
在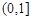 上的最小值为
上的最小值为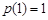 .
.所以实数
 的取值范围为
的取值范围为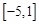 . ……………………………………… 9分
. ……………………………………… 9分(Ⅲ)解法一:
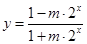 ,
, .
.∵
 ,
,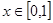 ,
,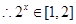 .
.∴
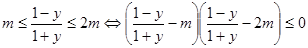
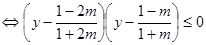 ,
,∵
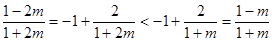
∴
 . …………………………………………… 11分
. …………………………………………… 11分①当
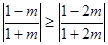 即
即 时,
时, 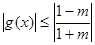 ,此时
,此时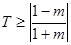 ;
;②当
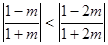 即
即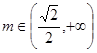 时,
时,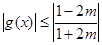 ,此时
,此时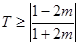 .
.综上所述,当
 时,
时, 的取值范围是
的取值范围是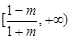 ;
;当
 时,
时, 的取值范围是
的取值范围是 ………… 14分
………… 14分解法二:
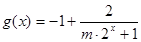 .令
.令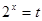 ,因为
,因为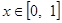 ,所以
,所以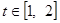 .
. .
.因为
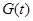 在
在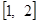 上是减函数,所以
上是减函数,所以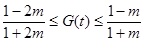 .………… 11分
.………… 11分又因为函数
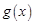 在
在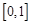 上的上界是
上的上界是 ,所以
,所以 .
.①当
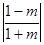
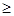
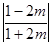 即
即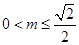 时,
时,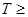
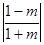
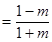 ;
;②当
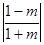
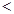
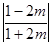 即
即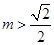 时,
时,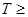
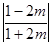
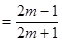 .…………… 14分
.…………… 14分略

练习册系列答案
相关题目
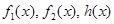 ,如果存在实数
,如果存在实数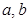 使得
使得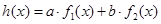 ,那么称
,那么称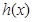 为
为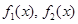 的生成函数.
的生成函数.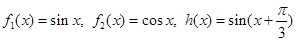 ;
;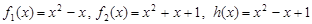 ;
; ,生成函数
,生成函数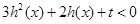 在
在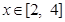 上有解,求实数
上有解,求实数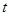 的取值范围;
的取值范围;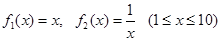 ,取
,取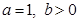 ,生成函数
,生成函数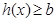 恒成立,求
恒成立,求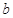 的取值范围.
的取值范围.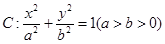 的离心率为
的离心率为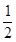 ,
,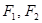 为椭圆的左右焦点,
为椭圆的左右焦点,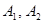 ;
;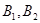 分别为椭圆的长轴和短轴的端点(如图) .若四边形
分别为椭圆的长轴和短轴的端点(如图) .若四边形 的面积为
的面积为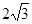 .
.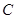 的方程.
的方程.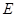
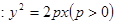 的焦点与椭圆
的焦点与椭圆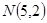 任意作一条直线
任意作一条直线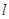 ,交抛物线
,交抛物线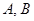 两点. 证明:以
两点. 证明:以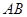 为直径的所有圆是否过抛物线
为直径的所有圆是否过抛物线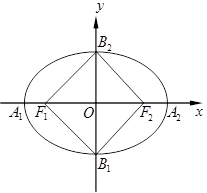
 =
= 的值域是 ( )
的值域是 ( ) g(x)=
g(x)= ,则函数h(x)= f (x)·g(x)
,则函数h(x)= f (x)·g(x)
 (注:
(注: )
) ,其中Pn为预测人口数,P0为初期人口数,k为预测年内增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么这期间人口数 ( )
,其中Pn为预测人口数,P0为初期人口数,k为预测年内增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么这期间人口数 ( ) ,则
,则 ( )
( ) 



 在区间
在区间 上是减函数,则实数
上是减函数,则实数 的取值范围是 .
的取值范围是 .