题目内容
.已知函数 的图象关于点
的图象关于点 对称,且函数
对称,且函数 为奇函数,则下列结论:(1)点
为奇函数,则下列结论:(1)点 的坐标为
的坐标为 ;(2)当
;(2)当 时,
时, 恒成立;(3)关于
恒成立;(3)关于 的方程
的方程 有且只有两个实根。其中正确结论的题号为( )
有且只有两个实根。其中正确结论的题号为( )
 的图象关于点
的图象关于点 对称,且函数
对称,且函数 为奇函数,则下列结论:(1)点
为奇函数,则下列结论:(1)点 的坐标为
的坐标为 ;(2)当
;(2)当 时,
时, 恒成立;(3)关于
恒成立;(3)关于 的方程
的方程 有且只有两个实根。其中正确结论的题号为( )
有且只有两个实根。其中正确结论的题号为( )| A.(1)(2) | B.(2)(3) | C.(1)(3) | D.(1)(2)(3) |
C
函数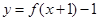 为奇函数,则其图像关于原点对称。而函数
为奇函数,则其图像关于原点对称。而函数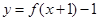 的图象可由
的图象可由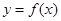 的图象向左平移1一个单位向下平移1个单位得到,所以函数
的图象向左平移1一个单位向下平移1个单位得到,所以函数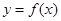 的图象关于
的图象关于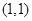 对称,所以点
对称,所以点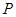 的坐标为
的坐标为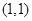 ,命题(1)正确;
,命题(1)正确;
因为函数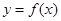 的图象关于
的图象关于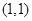 对称,而当
对称,而当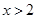 时
时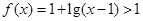 ,所以当
,所以当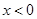 时,
时,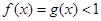 ,则存在
,则存在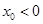 有
有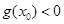 ,命题(2)不正确;
,命题(2)不正确;
当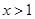 时,
时,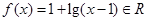 且单调递增,所以当
且单调递增,所以当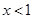 时,
时,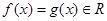 也单调递增。所以方程
也单调递增。所以方程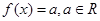 在
在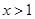 和
和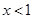 各有一解,命题(3)正确。
各有一解,命题(3)正确。
综上可得,选C
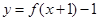 为奇函数,则其图像关于原点对称。而函数
为奇函数,则其图像关于原点对称。而函数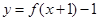 的图象可由
的图象可由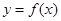 的图象向左平移1一个单位向下平移1个单位得到,所以函数
的图象向左平移1一个单位向下平移1个单位得到,所以函数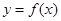 的图象关于
的图象关于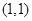 对称,所以点
对称,所以点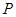 的坐标为
的坐标为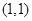 ,命题(1)正确;
,命题(1)正确;因为函数
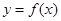 的图象关于
的图象关于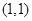 对称,而当
对称,而当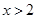 时
时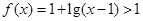 ,所以当
,所以当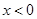 时,
时,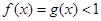 ,则存在
,则存在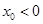 有
有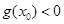 ,命题(2)不正确;
,命题(2)不正确;当
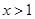 时,
时,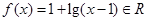 且单调递增,所以当
且单调递增,所以当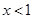 时,
时,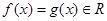 也单调递增。所以方程
也单调递增。所以方程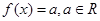 在
在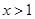 和
和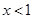 各有一解,命题(3)正确。
各有一解,命题(3)正确。综上可得,选C

练习册系列答案
相关题目
 件,请你写出
件,请你写出 之间的关系式;
之间的关系式; 的不等式
的不等式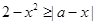 至少有一个负数解,则
至少有一个负数解,则 的最小值为_______.
的最小值为_______.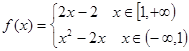 ,则函数
,则函数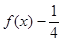 的零点为▲ .
的零点为▲ . =
= 的值域是 ( )
的值域是 ( ) 成立,则称f(x)[a,b]上的凸函数。试问:在下列图像中,是凸函数图像的为
成立,则称f(x)[a,b]上的凸函数。试问:在下列图像中,是凸函数图像的为
 时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的
时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的 .
.

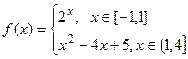
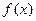 的图象;
的图象; 的方程组
的方程组 有唯一的一组实数解,则实数
有唯一的一组实数解,则实数 的值为_____________.
的值为_____________.