题目内容
证明:ln(n+1)<1+
+
+…+
(n∈正整数).
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
考点:不等式的证明
专题:综合题,不等式的解法及应用
分析:构造函数f(x)=ln(1+x)-x,利用导数法可证得ln(1+x)≤x(当x≠0时,ln(1+x)<x),令x=
,利用对数函数的运算性质及累加法求和即可证得结论成立.
| 1 |
| n |
解答:
证明:构造函数f(x)=ln(1+x)-x,
则f′(x)=
-1=
,
当-1<x<0时,f′(x)>0,f(x)在(-1,0)上单调递增;
当x>0时,f′(x)<0,f(x)在(0,+∞)上单调递减;
所以,当x=0时,f(x)=ln(1+x)-x取得极大值,也是最大值,
所以,f(x)≤f(0)=0,即ln(1+x)≤x,当x≠0时,ln(1+x)<x.
令x=
,
则ln(1+
)=ln(n+1)-lnn<
,即
>ln(n+1)-lnn,
∴1>ln2-ln1,
>ln3-ln2,
…
>lnn-ln(n-1)],
>ln(n+1)-lnn,
以上n个不等式相加得:1+
+
+…+
>ln(n+1)-ln1=ln(n+1)(得证).
则f′(x)=
| 1 |
| 1+x |
| -x |
| 1+x |
当-1<x<0时,f′(x)>0,f(x)在(-1,0)上单调递增;
当x>0时,f′(x)<0,f(x)在(0,+∞)上单调递减;
所以,当x=0时,f(x)=ln(1+x)-x取得极大值,也是最大值,
所以,f(x)≤f(0)=0,即ln(1+x)≤x,当x≠0时,ln(1+x)<x.
令x=
| 1 |
| n |
则ln(1+
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
∴1>ln2-ln1,
| 1 |
| 2 |
…
| 1 |
| n-1 |
| 1 |
| n |
以上n个不等式相加得:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
点评:本题考查不等式的证明,构造函数f(x)=ln(1+x)-x,利用导数法证得ln(1+x)≤x是关键,也是难点,考查创新思维、化归思想与推理论证能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
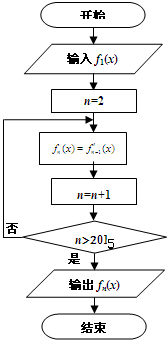 在程序框图中,当n∈N(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为( )
在程序框图中,当n∈N(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为( )A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列命题的说法错误的是( )
| A、命题“若x2-4x-3=0,则x=1”的逆否命题为“若x≠1,则x2-4x-3≠0” | ||||
| B、已知a,b,c是△A BC的三条边,△A BC是等边三角形的充要条件是a2+b2+c2=ab+ac+bc | ||||
C、命题“若α=
| ||||
| D、若命题p:b=0,命题q:函数f(x)=ax2+bx+c是偶函数,则p是q的充分不必要条件 |
如图是函数y=f(x)的导函数的图象,则正确的判断是( )
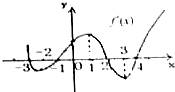

| A、f(x)在(-2,1)上是增函数 |
| B、x=1是f(x)的极大值点 |
| C、f(x)在(-1,2)上是增函数,在(2,4)上是减函数 |
| D、x=3是f(x)的极小值点 |
