题目内容
已知数列{an}的前n项和Sn=2n2+2n,数列{bn}的前n项和Tn=2-bn.
(1) 求数列{an}与{bn}的通项公式;
(2) 设cn=a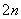 ·bn,证明:当且仅当n≥3时,cn+1<cn.
·bn,证明:当且仅当n≥3时,cn+1<cn.
(1) 解:a1=S1=4,当n≥2时,an=Sn-Sn-1=2n(n+1)-2(n-1)n=4n.
又a1=4适合上式,∴an=4n(n∈N*).
将n=1代入Tn=2-bn,得b1=2-b1,∴T1=b1=1.
当n≥2时,Tn-1=2-bn-1,Tn=2-bn,
∴bn=Tn-Tn-1=bn-1-bn,
∴bn= bn-1,∴bn=21-n.
bn-1,∴bn=21-n.
(2) 证明:证法1:由cn=a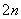 ·bn=n2·25-n,
·bn=n2·25-n,
得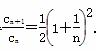
当且仅当n≥3时,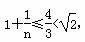 ,即cn+1<cn.
,即cn+1<cn.
证法2:由cn=a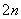 ·bn=n2·25-n,
·bn=n2·25-n,
得cn+1-cn=24-n[(n+1)2-2n2]=24-n[-(n-1)2+2].
当且仅当n≥3时,cn+1-cn<0,即cn+1<cn.

练习册系列答案
相关题目
 ,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率( )
,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率( ) B.
B.  C.
C.  D.
D.
 ,则S4=________.
,则S4=________. (n∈N*),bn=log2 an,则数列{bn}的前n项和Sn取最大时,n=________.
(n∈N*),bn=log2 an,则数列{bn}的前n项和Sn取最大时,n=________.