题目内容
14.${(2x+\frac{1}{{\sqrt{x}}})^5}$的展开式中,$\sqrt{x}$的系数为40.分析 利用通项公式即可得出.
解答 解:通项公式Tr+1=${∁}_{5}^{r}$(2x)5-r$(\frac{1}{\sqrt{x}})^{r}$=25-r${∁}_{5}^{r}$${x}^{5-\frac{3}{2}r}$,
令5-$\frac{3}{2}$r=$\frac{1}{2}$,解得r=3.
∴$\sqrt{x}$的系数=${2}^{2}{∁}_{5}^{3}$=40.
故答案为:40.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
5.已知i为虚数单位,则$\frac{1+2i}{1-i}$的共轭复数为( )
| A. | -$\frac{1}{2}$+$\frac{3}{2}$i | B. | $\frac{1}{2}$+$\frac{3}{2}$i | C. | -$\frac{1}{2}$-$\frac{3}{2}$i | D. | $\frac{1}{2}$-$\frac{3}{2}$i |
9.抛物线y2=4x的焦点为F,点A(3,2),P为抛物线上一点,且P不在直线AF上,则△PAF周长的最小值为( )
| A. | 4 | B. | 5 | C. | $4+2\sqrt{2}$ | D. | $5+\sqrt{5}$ |
6.已知函数f(x)在R上满足f(x)=2f(2-x)-x2+8x-8,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A. | y=-2x+3 | B. | y=x | C. | y=3x-2 | D. | y=2x-1 |
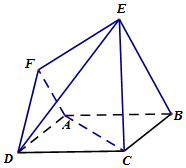 在如图所示的六面体中,面ABCD是边长为2的正方形,面ABEF是直角梯形,∠FAB=90°,AF∥BE,BE=2AF=4.
在如图所示的六面体中,面ABCD是边长为2的正方形,面ABEF是直角梯形,∠FAB=90°,AF∥BE,BE=2AF=4.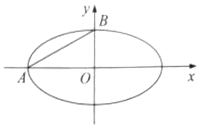 已知点A(-2,0),B(0,1)在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上.
已知点A(-2,0),B(0,1)在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上.