题目内容
11.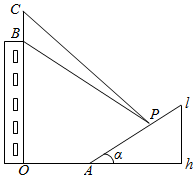 如图,某人在一小斜坡上的点P(坡高h=10m)观看对面一座大楼顶上的广告画,画高BC=8m,画所在的大楼高OB=22m,OA=20m,图上所示的山坡坡面可视为直线l,且点P在直线l上,l与水平地面的夹角为α,tanα=$\frac{1}{2}$.试问:此人所在的点P距水平地面多高时,观看广告画的视角∠BPC最大?(不计此人身高,楼OB与斜坡l在同一平面内)
如图,某人在一小斜坡上的点P(坡高h=10m)观看对面一座大楼顶上的广告画,画高BC=8m,画所在的大楼高OB=22m,OA=20m,图上所示的山坡坡面可视为直线l,且点P在直线l上,l与水平地面的夹角为α,tanα=$\frac{1}{2}$.试问:此人所在的点P距水平地面多高时,观看广告画的视角∠BPC最大?(不计此人身高,楼OB与斜坡l在同一平面内)
分析 过P作OB的垂线PM,设PM=x,用x表示出tan∠CPM,tan∠BPM,使用差角的正切公式求出tan∠CPB关于x的函数,使用基本不等式得出tan∠CPB的最值及等号成立的条件.
解答  解:过P点作PM⊥OB于M,设OM=x,(0≤x≤10),则BM=22-x,CM=30-x.PM=20+2x.
解:过P点作PM⊥OB于M,设OM=x,(0≤x≤10),则BM=22-x,CM=30-x.PM=20+2x.
∴tan∠CPM=$\frac{CM}{PM}$=$\frac{30-x}{20+2x}$,tan∠BPM=$\frac{BM}{PM}=\frac{22-x}{20+2x}$.
∴tan∠CPB=$\frac{tan∠CPM-tan∠BPM}{1+tan∠CPM•tan∠BPM}$=$\frac{\frac{30-x}{20+2x}-\frac{22-x}{20+2x}}{1+\frac{30-x}{20+2x}×\frac{22-x}{20+2x}}$=$\frac{16(x+10)}{5{x}^{2}+28x+1060}$=$\frac{16}{5(x+10)+\frac{1280}{x+10}-72}$≤$\frac{16}{2\sqrt{5×1280}-72}$=$\frac{2}{11}$.
当且仅当5(x+10)=$\frac{1280}{x+10}$即x=6时,tan∠CPB取得最大值,即∠CPB最大.
∴此人所在的点P距水平地面6m时,观看广告画的视角∠BPC最大.
点评 本题考查了解三角形,基本不等式,函数的最值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在距离2016年央视春晚直播不到20天的时候,某媒体报道,由六小龄童和郭富城合演的《猴戏》节目被毙,为此,某网站针对“是否支持该节目上春晚”对网民进行调查,得到如下数据:
若采用分层抽样的方法从中抽取48人进行座谈,则持“支持”态度的网民抽取的人数为16.
| 网民态度 | 支持 | 反对 | 无所谓 |
| 人数(单位:人) | 8000 | 6000 | 10 000 |
19.设tan(3π+θ)=a,则$\frac{sin(θ-5π)+cos(π-θ)}{sin(-θ)-cos(π+θ)}$的值为( )
| A. | $\frac{a+1}{a-1}$ | B. | $\frac{a-1}{a+1}$ | C. | $\frac{-a-1}{a-1}$ | D. | $\frac{-a+1}{a-1}$ |
6.若ω≠0,函数f(x)=$\frac{tanωx-\sqrt{3}}{\frac{\sqrt{3}}{3}+tanωx}$图象的相邻两个对称中心之间的距离是$\frac{π}{2}$,则ω的值是( )
| A. | $\frac{π}{2}$ | B. | ±2 | C. | 2 | D. | ±1 |
3.已知函数f(x)=$\frac{ln(2x)}{x}$,关于x的不等式f2(x)+af(x)>0只有两个整数解,则实数a的取值范围是( )
| A. | ($\frac{1}{3}$,ln2] | B. | (-ln2,-$\frac{1}{3}$ln6) | C. | (-ln2,-$\frac{1}{3}$ln6] | D. | ($\frac{1}{3}$ln6,ln2) |
20.函数f(x)=2x${\;}^{\frac{1}{3}}$的图象( )
| A. | 关于y轴对称 | B. | 关于x轴对称 | C. | 关于直线y=x对称 | D. | 关于原点对称 |