题目内容
20.函数f(x)=2x${\;}^{\frac{1}{3}}$的图象( )| A. | 关于y轴对称 | B. | 关于x轴对称 | C. | 关于直线y=x对称 | D. | 关于原点对称 |
分析 判断函数的奇偶性,然后推出结果即可.
解答 解:函数f(x)=2x${\;}^{\frac{1}{3}}$,满足f(-x)=-f(x),函数是奇函数,所以函数f(x)=2x${\;}^{\frac{1}{3}}$的图象关于原点对称.
故选:D.
点评 本题考查函数的奇偶性,函数的图象的对称性,是基础题.

练习册系列答案
相关题目
10.以下四个命题中正确的是( )
| A. | 命题“对任意的x∈R,x2≥0”的否定是“对任意的x∈R,x2≤0” | |
| B. | 命题“若x≥2且y≥3,则x+y≥5”的否命题为“若x<2且y<3,则x+y<5” | |
| C. | 记向量$\overrightarrow{a}$=(1,-1)与$\overrightarrow{b}$=(2,m)的夹角为θ,则“|$\overrightarrow{b}$|=$\sqrt{5}$”是“夹角θ为锐角”的充分不必要条件 | |
| D. | 记变量x,y满足的不等式组$\left\{\begin{array}{l}{-1≤x≤1}\\{0≤y≤2}\\{-x+y≥1}\end{array}\right.$表示的平面区域为D,则“k=-1”是“直线y=kx+1平分平面区域Dy=kx+1”的必要不充分条件 |
5.已知直线l∥平面α,l?平面β,α∩β=m,则直线l,m的位置关系是( )
| A. | 相交 | B. | 平行 | C. | 异面 | D. | 相交或异面 |
12.下列各组函数中,表示同一函数的是( )
| A. | y=x与y=$\sqrt{{x}^{2}}$ | B. | y=$\frac{x}{x}$与y=x0 | ||
| C. | y=($\sqrt{x}$)2与y=|x| | D. | y=$\sqrt{x+1}\sqrt{x-1}$与y=$\sqrt{{x}^{2}-1}$ |
9.已知sin(π-α)=a(-1<a<1),α是第四象限角,则cos(-π-α)的值为( )
| A. | $\sqrt{1-a^2}$ | B. | -$\sqrt{1+a^2}$ | C. | $\sqrt{1+a^2}$ | D. | -$\sqrt{1-a^2}$ |
16.投掷一颗骰子两次,将得到的点数依次记为a,b,则直线ax-by=0的倾斜角大于$\frac{π}{4}$的概率为( )
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
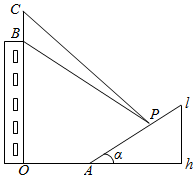 如图,某人在一小斜坡上的点P(坡高h=10m)观看对面一座大楼顶上的广告画,画高BC=8m,画所在的大楼高OB=22m,OA=20m,图上所示的山坡坡面可视为直线l,且点P在直线l上,l与水平地面的夹角为α,tanα=$\frac{1}{2}$.试问:此人所在的点P距水平地面多高时,观看广告画的视角∠BPC最大?(不计此人身高,楼OB与斜坡l在同一平面内)
如图,某人在一小斜坡上的点P(坡高h=10m)观看对面一座大楼顶上的广告画,画高BC=8m,画所在的大楼高OB=22m,OA=20m,图上所示的山坡坡面可视为直线l,且点P在直线l上,l与水平地面的夹角为α,tanα=$\frac{1}{2}$.试问:此人所在的点P距水平地面多高时,观看广告画的视角∠BPC最大?(不计此人身高,楼OB与斜坡l在同一平面内)