题目内容

17．已知等比数列{an}中，a1＜0，an+1＞an，则公比的取值范围是（0，1）．

分析 由已知可得：${a}_{1}{q}^{n}＞{a}_{1}{q}^{n-1}$，化为qn-1（q-1）＜0，解出即可得出．

解答 解：设等比数列{an}的公比为q，∵an+1＞an，
∴${a}_{1}{q}^{n}＞{a}_{1}{q}^{n-1}$，又a1＜0，
∴qn-1（q-1）＜0，
∴0＜q＜1，
故答案为：（0，1）．

点评 本题考查了等比数列的通项公式性质、不等式的性质，考查了分类讨论方法、推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
7．在等差数列{an}中，对任意正整数n，都有an+1+an=4n-4028，则a2015=2015．
8．已知函数f（x）=x2+4x+4，若存在实数t，当x∈[1，t]时，f（x+a）≤4x恒成立，则实数t的最大值为（　　）
A．4B．7C．8D．9
5．函数y=sinx•tanx的图象大致是（　　）
A．B．C．D．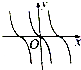
12．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F（1，0），过点F的直线l交椭圆C于M，N两点，圆x2+y2=$\frac{2}{3}$与椭圆C的四个顶点构成的四边形相切．
（1）求椭圆C的方程；
（2）证明：$\frac{1}{|MF|}$+$\frac{1}{|NF|}$为定值，并求出此定值．
2．过椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的准线上动点M引圆O：x2+y2=b2的两条切线MA，MB．其中A，B分别为切点，若存在点M，使△ABM为正三角形，则该椭圆的离心率的取值集合为{$\frac{\sqrt{2}}{2}$}．
9．在等差敦列（an}中，a2=3，a7=13，数列{bn}的前n项和为Sn，且Sn=$\frac{4}{3}$（4n-1）．
（1）求an及bn；
（2）求数列{an•bn}的前n项和Tn．
6．在平面直角坐标系xOy中，已知角β的顶点为坐标原点O，始边在x轴的正半轴上，终边经过点P（-4，3）
（1）求sinβ与sin2β的值
（2）已知函数f（x）=3cos（x-$\frac{π}{4}$），求函数f（x）的最大值和最小正周期，并求f（β）的值．
18．已知$sin（\frac{π}{6}-α）=cos（\frac{π}{6}+α）$，则tanα=（　　）
A．-1B．0C．$\frac{1}{2}$D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网