题目内容
18.已知$sin(\frac{π}{6}-α)=cos(\frac{π}{6}+α)$,则tanα=( )| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
分析 利用两角和与差的正弦函数,余弦函数公式,特殊角的三角函数值化简已知可得$\frac{1-\sqrt{3}}{2}$cosα=$\frac{\sqrt{3}-1}{2}$sinα,利用同角三角函数基本关系式即可计算求值tanα.
解答 解:∵$sin(\frac{π}{6}-α)=cos(\frac{π}{6}+α)$,
∴$\frac{1}{2}$cosα-$\frac{\sqrt{3}}{2}$sinα=$\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα,
∴$\frac{1-\sqrt{3}}{2}$cosα=$\frac{\sqrt{3}-1}{2}$sinα,
∴tanα=$\frac{sinα}{cosα}$=$\frac{\frac{1-\sqrt{3}}{2}}{\frac{\sqrt{3}-1}{2}}$=-1.
故选:A.
点评 本题主要考查了两角和与差的正弦函数,余弦函数公式,特殊角的三角函数值,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,且3$\overrightarrow{a}$+2$\overrightarrow{b}$与λ$\overrightarrow{a}$-$\overrightarrow{b}$垂直,则实数λ的值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | ±$\frac{3}{2}$ | D. | 1 |
3.设全集U=R,集合A={x|7-6x≤0},集合B={x|y=lg(x+2)},则(∁UA)∩B等于( )
| A. | (-2,$\frac{7}{6}$) | B. | ($\frac{7}{6}$,+∞) | C. | [-2,$\frac{7}{6}$) | D. | (-2,-$\frac{7}{6}$) |

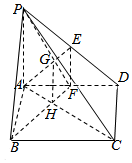 如图,在底面为正方形的四棱锥P-ABCD中,PA⊥底面ABCD,AP=AD,取线段PD,AD的中点E,F,连结AE,PF交于一点G.连结BF交AC于点H.
如图,在底面为正方形的四棱锥P-ABCD中,PA⊥底面ABCD,AP=AD,取线段PD,AD的中点E,F,连结AE,PF交于一点G.连结BF交AC于点H.