题目内容
下列函数既是奇函数又是增函数的是( )
| A、y=-x |
| B、y=x+1 |
| C、y=x2 |
| D、y=x3 |
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:选项中所涉及到的函数既是奇函数又是增函数的符合条件,要从两个方面进行判断.这两个方面可以借助于图象,也可以直接利用奇函数的定义和函数单调性的判定方法进行求解.
解答:
解:选项A中,函数y=-x是奇函数并且为减函数,不符合题意;
选项B中,设函数y=f(x),
∵f(-x)≠±f(x),
∴函数y=x+1为非奇非偶函数,
∴选项B 不符合题意;
选项C中,
∵f(-x)=f(x),
∴函数y=x2则为偶函数,
选项C不符合题意;
只有选项D符合条件,
故选D.
选项B中,设函数y=f(x),
∵f(-x)≠±f(x),
∴函数y=x+1为非奇非偶函数,
∴选项B 不符合题意;
选项C中,
∵f(-x)=f(x),
∴函数y=x2则为偶函数,
选项C不符合题意;
只有选项D符合条件,
故选D.
点评:本题重点考查常见函数的单调性和奇偶性,注意它们的判定方法.

练习册系列答案
相关题目
双曲线
-
=1的渐近线为y=±3x,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
函数f(x)=sin(ωx+φ)(ω>0,-
<φ<
)的部分图象如图所示,则φ的值为( )

| π |
| 2 |
| π |
| 2 |

A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知{an}为等差数列,且a2+a8=8,a6=5,则Sl0的值为( )
| A、50 | B、45 | C、55 | D、40 |
已知集合M={x∈R||x|>2},N={x∈R|x2-4x+3<0},则集合(∁RM)∩N 等于( )
| A、{x|x<2} |
| B、{x|-2≤x≤2} |
| C、{x|-2≤x<1} |
| D、{x|1<x≤2} |
已知函数f(x)=2|x|,那么函数f(x)( )
| A、是奇函数,且在(-∞,0)上是增函数 |
| B、是偶函数,且在(-∞,0)上是减函数 |
| C、是奇函数,且在(0,+∞)上是增函数 |
| D、是偶函数,且在(0,+∞)上是减函数 |
下列说法中错误的是( )
| A、如果命题“¬p”与命题“p∨q”都是真命题,那么命题q一定是真命题 |
| B、命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0” |
| C、若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1≥0 |
| D、“a=2”是“直线ax+2y=0平行于直线x+y=1”的充分不必要条件 |
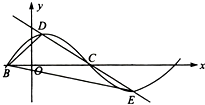 已知函数f(x)=sin(2πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(
已知函数f(x)=sin(2πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(