题目内容
已知α为第四象限角，sinα+cosα=
，则cos2α= ．
| 2 |
| 3 |
考点：二倍角的余弦,三角函数的化简求值
专题：三角函数的求值
分析：利用二倍角的正弦与同角三角函数间的关系可求得cosα-sinα=
，再利用二倍角的余弦即可求得cos2α．
| ||
| 3 |
解答：
解：∵sinα+cosα=
，①
∴两边平方得：1+2sinαcosα=
，
∴2sinαcosα=-
＜0，
∵α为第四象限角，
∴sinα＜0，cosα＞0，cosα-sinα＞0．
∴cosα-sinα=
=
，②
∴①+②可解得：cosα=
，
∴cos2α=2cos2α-1=2×（
）2-1=
．
故答案为：
．
| 2 |
| 3 |
∴两边平方得：1+2sinαcosα=
| 4 |
| 9 |
∴2sinαcosα=-
| 5 |
| 9 |
∵α为第四象限角，
∴sinα＜0，cosα＞0，cosα-sinα＞0．
∴cosα-sinα=
| 1-2sinαcosα |
| ||
| 3 |
∴①+②可解得：cosα=
2+
| ||
| 6 |
∴cos2α=2cos2α-1=2×（
2+
| ||
| 6 |
2
| ||
| 9 |
故答案为：
2
| ||
| 9 |
点评：本题考查二倍角的正弦、余弦与同角三角函数间的关系，属于中档题．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
设集合M={0，1}，N={x∈Z|y=
），则（ ）
| 1-x |
| A、M∩N=∅ |
| B、M∩N={0} |
| C、M∩N{1} |
| D、M∩N=M |
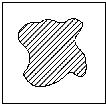如下图，边长为2的正方形中有一阴影区域，在正方形中随机撒一粒豆子，它落在阴影区域内的概率为| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
| D、无法计算 |
已知函数f（x）=（
a-
）sinx+（
a+1）cosx，将f（x）图象向右平移
个单位长度得到函数g（x）的图象，若对任意x∈R，都有g（x）≤|g（
）|成立，则a的值为（ ）
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| π |
| 3 |
| π |
| 4 |
| A、-1 | B、1 | C、-2 | D、2 |
已知数列{an}是等比数列，且a2+a6=3，a6+a10=12，则a8+a12=（ ）
A、12
| ||
| B、24 | ||
C、24
| ||
| D、48 |
已知等比数列{an}中，a1=4，且a4a6=4a72，则a3=（ ）
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|