题目内容
一个圆柱的母线长度为1，底为半径为1的圆，则此圆柱的侧面积是（ ）
| A、π | B、2π | C、3π | D、4π |
考点：旋转体（圆柱、圆锥、圆台）
专题：计算题,空间位置关系与距离
分析：圆柱侧面积=底面周长×高．由此利用题设条件能够求出结果．
解答：
解：圆柱沿一条母线剪开，所得到的侧面展开图是一个矩形，
它的长是底面圆的周长，即2π，宽为母线长为1，
所以它的面积2π．
故圆柱的侧面积为2π．
故选：B．
它的长是底面圆的周长，即2π，宽为母线长为1，
所以它的面积2π．
故圆柱的侧面积为2π．
故选：B．
点评：本题考查了圆柱的计算，掌握特殊立体图形的侧面展开图的特点，是解决此类问题的关键．
练习册系列答案
相关题目
在等差数列{an}中，若a1+a13=12，则a7为（ ）
| A、6 | B、7 | C、8 | D、9 |
复数（
+
i）3（i为虚数单位）的值是（ ）
| 1 |
| 2 |
| ||
| 2 |
| A、-1 | B、1 | C、-i | D、i |
正方体ABCD-A1B1C1D1中，异面直线B1D1与DC1所成角的大小是（ ）
| A、30° | B、60° |
| C、45° | D、90° |
下面四个命题：
①a，b是两个相等的实数，则（a-b）+（a+b）i是纯虚数；
②任何两个复数不能比较大小；
③若z1，z2∈C，且z12+z22=0，则z1=z2=0；
④两个共轭虚数的差为纯虚数．
其中错误的个数有（ ）
①a，b是两个相等的实数，则（a-b）+（a+b）i是纯虚数；
②任何两个复数不能比较大小；
③若z1，z2∈C，且z12+z22=0，则z1=z2=0；
④两个共轭虚数的差为纯虚数．
其中错误的个数有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
甲乙丙三位同学独立的解决同一个问题，已知三位同学能够正确解决这个问题的概率分别为
、
、
，则有人能够解决这个问题的概率为（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
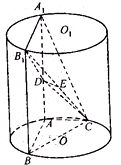如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D、E分别是AA1、CB1的中点，AB=AC．